What Would Kant Think of LLMs?
Introduction
In the late 1700s, the great German philosopher Immanuel Kant revolutionized his field through the work Critique of Pure Reason. This was probably the most significant advance in philosophy since the time of the Greeks and has influenced the course of the subject since the time it was published. Around the same time modern science was also making great strides. It emerged in the 17th century with luminaries such as Galileo and Newton but charted its own course independent of philosophy. In part this was due to the separation between science and the mind that was put into place by the great French thinker Descartes, at the dawn of the Scientific Age. The separation finally started break down in the 20th century when it became clear that the new science of Quantum Mechanics had some deep problems if we try to interpret it within the existing scientific framework, which didn’t take the mind into account.
In our century we have another emerging science (or is Technology?) of Artificial Neural Networks (ANNs) and the attendant subfield of Large Language Models (LLMs). The latter serve as models for human language and there are open questions whether these models are actually modeling human cognition. A deeper understanding of a proper framework for science that takes both the mind as well as ANNs into account has become important due to these developments. Getting a better understanding of how mathematical models, whether in physics or in Artificial Intelligence, and how they relate to reality and our perceptions of reality is critical in resolving these questions. Several new ideas in these areas have been proposed in the last two decades and it seems that some of Kant’s thinking is again starting to become very relevant. We have finally started to make some progress with problems ranging from the interpretation of Quantum Mechanics to theories of how the mind works. In this essay I will start by surveying the state of knowledge in these fields, followed by some ideas on how these can be applied to the interpretation of mathematical models for language in the form of LLMs.
Here is a brief definition of the main actors in this drama:
- Base Reality (sometimes also called Objective Reality): This is reality as it exists independent of human perception.
- Perceived Reality: Information from Base Reality impinges on our senses, and our brain puts it all together to create the world as we see, hear and feel it.
- Mathematics and Mathematical Models: Mathematics can be defined as a self-consistent system of thought, operating using the rules of logic. It can be used to create models of reality, as was discovered by Galileo and Newton more than 300 years ago.
- Science: These serve as models of perceived reality and constructed using models which can be mathematical in the case of physics, or chemical in the case of biology.
- The Brain: Our brain consists of a large number of interconnected neurons, which is somehow able to generate the mind and all the subjective experiences that go along with it.
- Artificial Neural Networks: These are also mathematical models, but of a special kind since they serve as models for the brain. These models are very different than the classical Newtonian models that are used in physics.
The Kantian Framework
Immanuel Kant set out for himself the task to discovering the limits of human knowledge and the result was his book “Critique of Pure Reason”, that was published almost 250 years ago. At the time of Kant, there was a debate in philosophical circles about the nature of our perception of the world. The philosophical school of Idealism, whose most prominent proponent was Bishop Berkeley (but also had predecessors such as Ancient Indian Philosophy and the Neo-Platonic School of Greek philosophy) claimed that the mind is the ultimate source of reality, and not physical stuff or matter. The other school was that of Realism which and it said that there is in fact an objective reality that exists independent of our minds, and what we see around us is like a window into that reality. Kant’s innovation was to propose a middle way between these philosophies, which he called Transcendental Idealism. According to it, our perception of the world incorporates elements from two sources:
- Source 1 is the information coming to us from the external world to our sensory organs. Hence there is an external world that does exist out there, unlike what the Idealists claimed, but we don’t have direct access to it using our senses (hence the Transcendentalism). Kant called this the Noumenon.
- Source 2 comes from our brain, which processes the information from Source 1 and generates a picture of the world as we perceive it, called the Phenomenon. However, this picture does not reflect the Noumenon or base reality, but is a creation of our brain, and it does so with the main objective of helping us survive.
This idea does get a little getting used to when we first encounter it, and it is difficult to believe that we are seeing around us is coming from within us, as opposed to existing out there. It requires a change in perspective which Kant called the Copernican Revolution in philosophy, since the idea that the Sun is stationary and that the Earth is going around is similarly difficult to grasp since it goes against our senses.
Fundamental to our perception of the world are the concepts of space (or the fact that objects have an extension in space) and time (or the fact that events have a duration in time). Kant claimed that space and time are purely concepts created by our brain (or a priori concepts) to bring order to the chaos of information coming to our senses, and do not exist in the Noumenon. Our perceptions are not things in the world, they are versions of those things that we construct in our minds by shaping them in space and time. Hence what we perceive is the world that our brain creates using the information from the Noumenon coming through our senses. However, this information is very different than the world that we actually perceive, for example when we see a red object in front of us, the sensation of redness is not part of the photons of light coming from that object. It is generated by our mind perhaps as a way to differentiate objects.
Kant did not argue for the existence of the Noumenon using empirical experiments, but instead relied on rhetoric and philosophical arguments. His main arguments are known as Kant’s Antinomies which are logical contradictions that arise when we confuse the phenomenal world and the noumenal world. Since the time of Kant the idea of the Noumenon has been much debated. Philosophers such as Hegel and Nietzsche have objected to the way Kant separated the world into two layers, and they said that since the Noumenon is effectively unknowable, it is irrelevant to practical philosophy. Other philosophers such as Schopenhauer accepted this idea and tried to develop it further.
The book ” The Rigor of Angels: Borges, Heisenberg, Kant and the Ultimate Nature of Reality” has an excellent description of the main elements of Kant’s philosophy, and also has a fascinating discussion of the similarities between it, the short stories of the Argentinian writer Jorge Luis Borges and basic ideas behind Quantum Mechanics as formulated by Werner Heisenberg. The following discussion of Kant’s ideas borrows from the presentation in this book:
For sensory input to become knowledge of the world requires that objects be located in respect to other things and that events be sequenced as coming before, after or simultaneous to other events. But locating objects with respect to one another in space, or sequencing events in time, is something that pure sense perception on its own cannot accomplish. This exposure needs to be organized in order to experience it. In order to experience the spatial relations between objects we implicitly assume that they exist together in a shared space. However, space itself is not an object of experience, but the very condition for experiencing objects. Space (and time) are like representations that our brain creates so that we can experience reality.
We make a fundamental error by assuming that space and time are objects in themselves that exist in Base Reality, just like other objects that we see around us. But instead, space and time are created by our brains as a way to mediate between the chaotic amount of data that is constantly impinging on our senses, by organizing them within this space-time framework or representation. Several classical paradoxes, such as that of Zeno, arise because of our tendency to treat space-time as a real object, followed by our application of the mathematical idea of infinite divisibility, to conclude that space-time can be divided into smaller and smaller segments infinitely many times. However, the idea of infinite divisibility is also not part of the Phenomenon, it exists purely in the world of mathematical concepts. The Laws of Physics are really the laws of our observations of how things behave in our Perceived Reality. There is a very nice quote by Heisenberg in this regard: “We have to remember that what we observe is not nature in itself but nature exposed to our method of questioning”.
A nice metaphor for Kant’s ideas of space-time is the way in which we use Cartesian co-ordinates to represent objects in geometry. Clearly the co-ordinate system is not another object, but instead it is an abstraction used to organize the objects that exist in mathematical space. Morever the co-ordinate system is not unique, in the sense that we can choose some other system, such as polar co-ordinates if we think that it supplies a better representation.
Once we accept the idea that space-time is not part of the Noumenon, but instead are constructs created by our brains to organize sensory data, then the question arises, what exactly is in the Noumenon? To this Kant’s response is: We don’t know, and we can never know. In order to perceive the Noumenon, we would need the ability to operate outside the limitations of space and time. However, all of our knowledge comes from operating within the limitations of time and space. Operating outside it would mean seeing everything simultaneously or knowing all of time in an instant, which would obliterate the very connection between objects and instances that constitutes knowledge. Since an observation is always an observation in time and space, the Laws of Physics are all about operations in time and space. We may speculate about the world outside the conditions of time and space, but nontemporal and nonspatial perspectives obliterate the very idea of an observation, and hence are incompatible with any knowledge we can have of the world.
Kant’s ideas came before the discovery of Quantum Mechanics and Relativity, and so a natural question is how well they have held up in light of these theories. The short answer is that that they have held up quite well. Heisenberg was inspired by the ideas of Kant in creating his Matrix Mechanics. He derived his equations with the purpose of explaining the world as it appears to our senses (and scientific instruments) and did not to try to visualize a human comprehensible model that lies behind those equations, a decidedly Kantian approach. Indeed, he later come up with the idea of the Uncertainty Principle that showed that our ideas of position and momentum do not extend to the microscopic world. Electrons and other microscopic entities are not objects in the sense that we see around us, and it is impossible for us to visualize what they are, since they appear either as particle or a wave depending upon the experiment we perform. This sounds a little bit like Kant’s ideas of the Noumenon, since that too contains objects that we can’t visualize. However, there is difference between the two, namely that the microscopic objects still exist within the framework of space-time and their properties can be accessed using scientific instruments and hence cannot be part of the Noumenon. They are still part of the Phenomenon, but these entities are so outside the realm of our daily experience that our language does not have the words to describe them and the only way to talk about them is by using the language of mathematics. Einstein himself never reconciled to the idea that the models in physics were not describing a base reality, hence is oft quoted remark that “God does not play dice with the universe” when he was confronted by the indeterminism in the predictions of Quantum Theory. Another relatively recent development is the Wheeler-Dewitt equation which is an area of active research in efforts to reconcile Gravity with Quantum Mechanics. Interestingly enough this equation does not have time as a variable, which is in line with Kant’s thinking.
The other domain of science that might shed light on the existence of the Noumenon is Cognitive Science, which is the study of how the neurons in our brain process information. Later in this blog we will describe one of the theories in this area by the neuro-scientist Anil Seth that was proposed recently. This theory has a decidedly Kantian flavor to it and tries to account for visual perception (and lots of other functions of the mind) using ideas whose origin can be traced back to Kant.
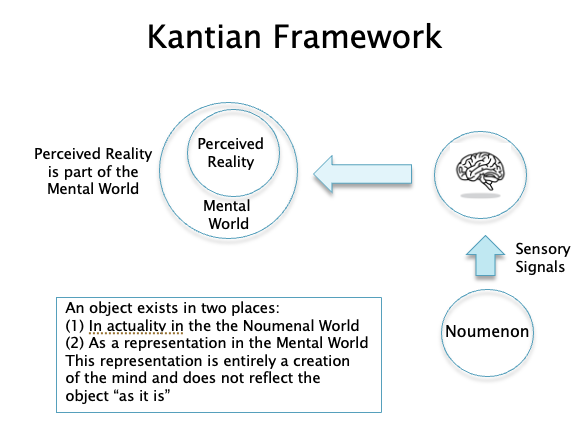
Figure 1
Fig. 1 summarizes Kant’s views: It shows signals such as light and sound waves coming from the Noumenon which impinge on our senses. These are then processed by the brain, which abstracts the deluge of data, and generates a picture of reality for us which is tailored so as to help us survive in our environment. Since all data coming from the Noumenon is filtered through the brain, we do not have direct access to the Noumenon.
Philosophical Frameworks for Science
Kant’s ideas were developed about a hundred years after the start of modern science with Descartes, Newton and Galileo. Science initially developed and made progress using a different framework than the one proposed by Kant, called Cartesian Dualism. This framework achieved great success and has given us the modern world. However as described later in the section, it has run into problems in recent times, which have led people to re-examine the basic ideas behind the framework.
Galileo and Newton made a monumental discovery more than 400 years ago, which is that the Laws of Nature lend themselves to a mathematical description. This adds another actor to our drama, namely the space of Mathematical Systems. What is a Mathematical System? These are systems that contain numerical or geometric objects, that are defined solely by the way they interact with other objects. The interaction is in terms of mathematical operations (that differ from system to system). The work of mathematicians consists of deriving interesting properties of the system using the rules of logic. At one time it was thought that Mathematical Systems reflect our reality, in the sense that the objects and rules in the system were abstractions of things that exist the real world. However this prejudice was exploded in the 19th century when mathematicians came up with Non-Euclidian Geometries and Number Systems that have nothing to do with our reality, but were studied purely because they resulted in interesting mathematical results. Some of these systems later found applications in modeling nature, much to the surprise of scientists.
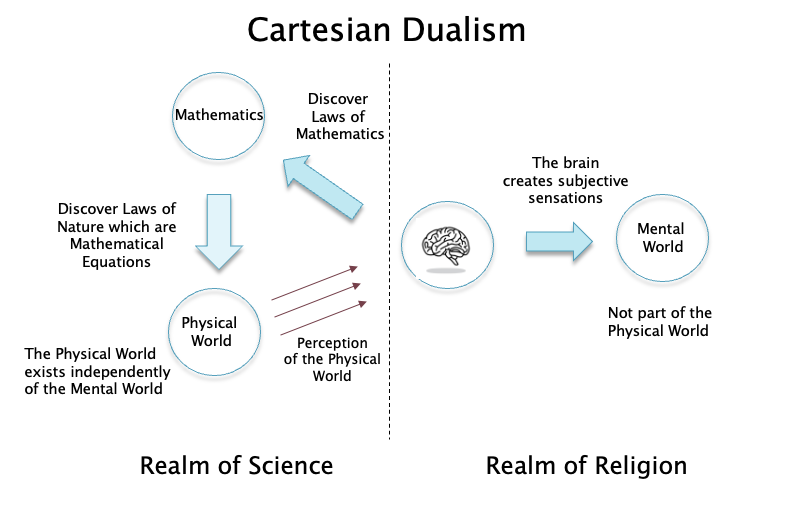
Figure 2
Our tale begins with Rene Descartes, the founder of Co-ordinate Geometry, which was one of his many achievements. Descartes also came up with the idea of Cartesian Dualism as the philosophical foundation for science, which is illustrated in Fig. 2. His big idea was to banish the mind from within the domain of science so that explanations for the mind and its subjective sensations were placed outside the scope of science. Instead, science was to limit itself to modeling the objective aspects of nature which could be measured in a precise manner using instruments. Descartes was motivated by several objectives in making this proposal. One big motivation was probably to keep the mind outside the scientific purview and make it part of the religious world, which was probably wise given what had happened to Bruno and Galileo around the same time that Descartes lived. Another motivation was to accelerate the progress of science by limiting it to explaining aspects of nature which could be measured in an objective fashion.
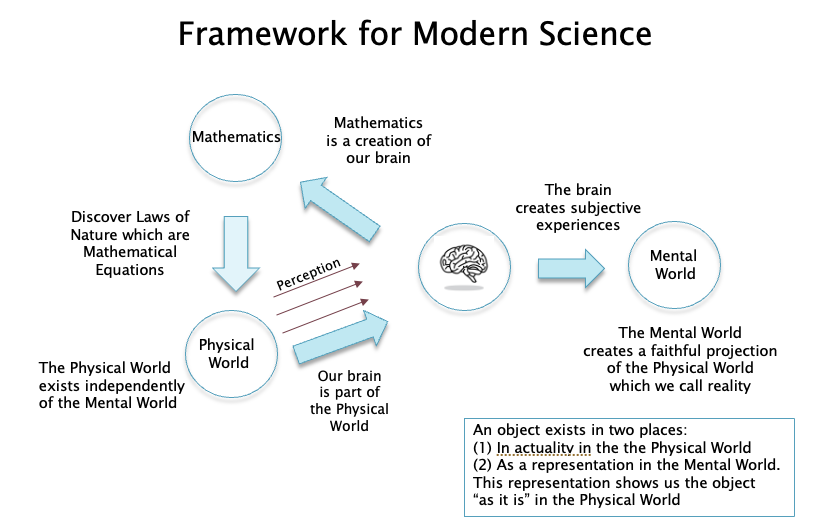
Figure 3
The Cartesian Framework for science has undergone a few changes since the seventeenth century, especially after the Age of Enlightenment in the 1700s, it was no longer taboo to include the mind as part of the framework. The generally accepted modern framework for science is well described by the eminent physicist Roger Penrose in his book “The Road to Reality”, and is shown in Fig. 3. This framework (which we will refer to as the post-Cartesian framework, it is also called Scientific Realism) states that:
- There is an entity called the physical world which has its own objective reality independent of the mental world.
- Our brain is one of the objects that exists in the physical world and it also allows us to perceive the physical world. This perception is like a window to the physical world and reflects a true picture of what exists in it.
- Certain aspects of the physical world can be objectively measured and abstracted, and these are part of science. These include quantities such as mass, momentum, electric charge etc.
- There is a world of mathematical objects, that is a creation of the human mind and a subset of this world serves as a model for the abstract measurements of the physical world. A stronger version of this belief is that the physical world at its core is nothing else but a set of mathematical equations (for an example of this see the book “Our Mathematical Universe” by Max Tegmark).
- Since other aspects of the physical world can be modeled using science, it should be possible to come up with a model for the brain which can explain the properties of the mind.
The post-Cartesian framework was highly successful in discovering laws that govern the physical world. After the initial development of Newtonian Dynamics, other aspects of nature such Electromagnetic Waves and the Laws of Thermodynamics were discovered in the 19th century, and they all fell within this framework (though electromagnetic theory is based on the concepts of electric and magnetic fields that Maxell and other scientists struggled to visualize using mechanical models). The first crack in the framework happened in the beginning years of the 20th century, with the discovery of energy quanta by Max Planck. Within a few years of that, Einstein proposed that light exhibits both wave and particle properties, and indeed within a couple of decades experiments were conducted that showed that material particles like electrons also have wavelike properties such frequency. This raised a conundrum since for the first time the fundamental constituents of nature had a form that could not be visualized by us humans. Soon after this Heisenberg followed by Schrodinger proposed a mathematical description of microscopic phenomena that was unlike any theory that had come before. Schrodinger’s version of the theory was based on a fundamental quantity called the wave function (or $\psi(x,t)$) whose nature was completely mysterious. After a lot of debate, Max Born proposed that the square of the wave function gives the probability distribution for the quantum particle being to be found in a certain volume of space, which meant that the dynamics of microscopic particles are fundamentally random.
In parallel several interpretations of Quantum Mechanics were proposed, the most prominent being what is called the Copenhagen Interpretation. This does not try to explain the wave-particle duality, but simply states that the particle can exhibit either depending upon the experiment being performed. A quantum particle that is not being observed can be in a superposition of several states at the same time and does not settle into a definite state until it is observed. This leads to the paradox of Schrodinger’s Cat being dead and alive at the same time (this has been tested experimentally with the Aspect experiments which resulted in the 2022 Nobel Prize in Physics, not with a cat though :-)). The Copenhagen Interpretation also states that the wave function is an objective (i.e., observer independent) measure of the uncertainty that we have about the Quantum World, and this uncertainty vanishes for objects in the macro world, in other words Quantum Mechanics comes into effect for microscopic objects but is not relevant at normal scales. This last claim of the Copenhagen Interpretation has been experimentally shown to be false recently, so that even larger objects can exhibit wave particle duality.
The Copenhagen Interpretation is a way to shove the interpretive problems in Quantum Theory under the rug, and proceed with the day-to-day applications of the theory and that has worked work well in practice. However, one can think of experiments in which the Copenhagen Interpretation fails, and the most well-known of these is known as the problem of Wigner’s Friend, which is as follows: Assume that there is a closed box containing a quantum particle that can be in one of two states, and an Observer 1 who is located outside the box. In addition, the system containing the box and Observer 1 is itself in a larger box which is closed to the outside. There is also a second observer, say Observer 2 (Wigner’s friend) who is located outside the larger box. Let’s say Observer 1 at some point opens the box and finds that the particle is in State 1, at this point the Wave Function from Observer 1’s point of view has ‘collapsed’ since there is no more uncertainty about the state of the particle. However, Observer 2 does not know this, and from his point of view, the combined system consisting of the particle and Observer 1 can be one of several possible quantum states. From this experiment it follows that there is no single observer independent interpretation of the wave function, i.e., the wave function is a subjective measure of uncertainty in a quantum system, and cannot be separated from the observer. This is precisely the Quantum Bayesianism or Qbism interpretation of Quantum Mechanics that was proposed recently. According to Qbism the wave function is a subjective measure of quantum uncertainty and exists only in the mind of the observer, and is not really part of physical reality as such. This strikes at the heart of the post-Cartesian Framework since we can no longer claim that science is discovering Laws of Nature that exist independent of our mind. Hence the QBism interpretation of Quantum Mechanics clearly does not fall within the traditional scientific framework shown in Fig. 3 and opens the door to examining Kant’s ideas as an alternative, which is discussed in the next section. A good description of these topics can be found in Chapter 5 of the book “Putting Ourselves Back in the Equation” by George Musser.
Other problems with the post-Cartesian framework for science emerge when we try to use it to explain the mind. The framework actually opens up the possibility of modeling the brain using mathematical models since the framework says that the brain is part of the physical world and since the mind arises from the brain, we should be able to model it using the rules of science. This raises the question: What is the right model for the brain and how can a set of physical processes happening within the brain give rise to our mind and its subjective experiences?
And therein lies the great mystery: If the brain indeed opens a window into reality and shows us the world “as is”, then how can we explain subjective experiences such as the sensation of the color, thirst, hunger, anger, joy etc. (collectively called qualia) since clearly these are not things that exists in the physical world. This failure to account for subjective sensations within the post-Cartesian framework is referred to as the “Hard Problem of Consciousness” in philosophy. In order to explain the mind, perhaps we need to go beyond the post-Cartesian Framework, just as Qbism did for Quantum Mechanics. In the next section we discuss in detail whether the Kantian Framework can solve the problems that are inherent in the post-Cartesian Framework.
A Kantian Framework for Science
In the previous section we described how the equations of Quantum Mechanics don’t describe an objective observer independent reality, but instead provide predictions that are tied to the mind of the observer doing the experiment. This appears very much like the picture of the world that Immanuel Kant drew in his philosophy. In this section we pursue this line of thinking, and also investigate how the Kantian Framework can be applied to models of the brain.
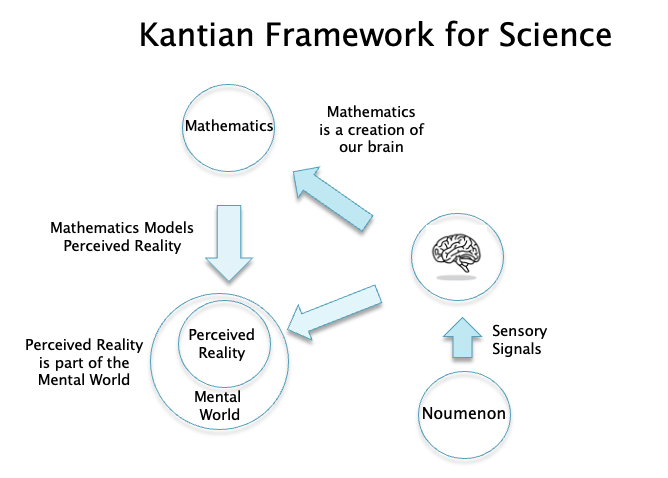
Figure 4
A Kantian framework of science is shown in Fig. 4. There is no longer a split between the Physical World and the Mental World as in Fig. 3, since our perceptions of reality are a creation of our brains and hence are part of the Mental World. The mathematical theories that we come up with do not describe the base reality or the Noumenon, but are instead modeling the subjective perceptions created by our minds. This might also explain why mathematics is so effective in scientific models, this is because both mathematics and perceived reality are creations of our minds.
An interesting aspect of this framework is that mathematical models of nature are no longer considered to be a reflection of some deep-seated objective reality that exists independent of our perception. If so, what are they? Why are they so good at predicting the operation of the world? A way to interpret these models is by using an idea called Instrumentalism, which basically says that mathematical models are a way to capture the regularities in our observations, nothing more than that. The main proponent of this point of view was the Austrian physicist Ernst Mach, who was a big influence on both the early Einstein and Heisenberg. In the process of deriving the equations of science, the scientist may hypothesize some underlying mechanism, such as the idea of fields to explain electromagnetism. But these are a mathematical convenience and do not reflect any underlying reality. In the next section we will see that mathematical models for the mind carry this way of thinking further, such that the models are essentially a black box connecting inputs to desired outputs. For a deeper dive into this idea, please see my blog post “Artificial Neural Networks and the Scientific Method”.
The QBism interpretation of Quantum Mechanics clearly falls within the Kantian Framework, since both say that the practice of science, at the most fundamental level, is a purely subjective endeavor. But what about theories of the mind? There have been proposals for theories of how the brain works which operate within the Kantian framework. The German scientist Herman von Helmholtz proposed one such theory in the late nineteenth century according to which the contents of perception are not given by sensory signals themselves but have to be inferred by the brain by combining these signals with the brain’s expectations or beliefs about their causes.
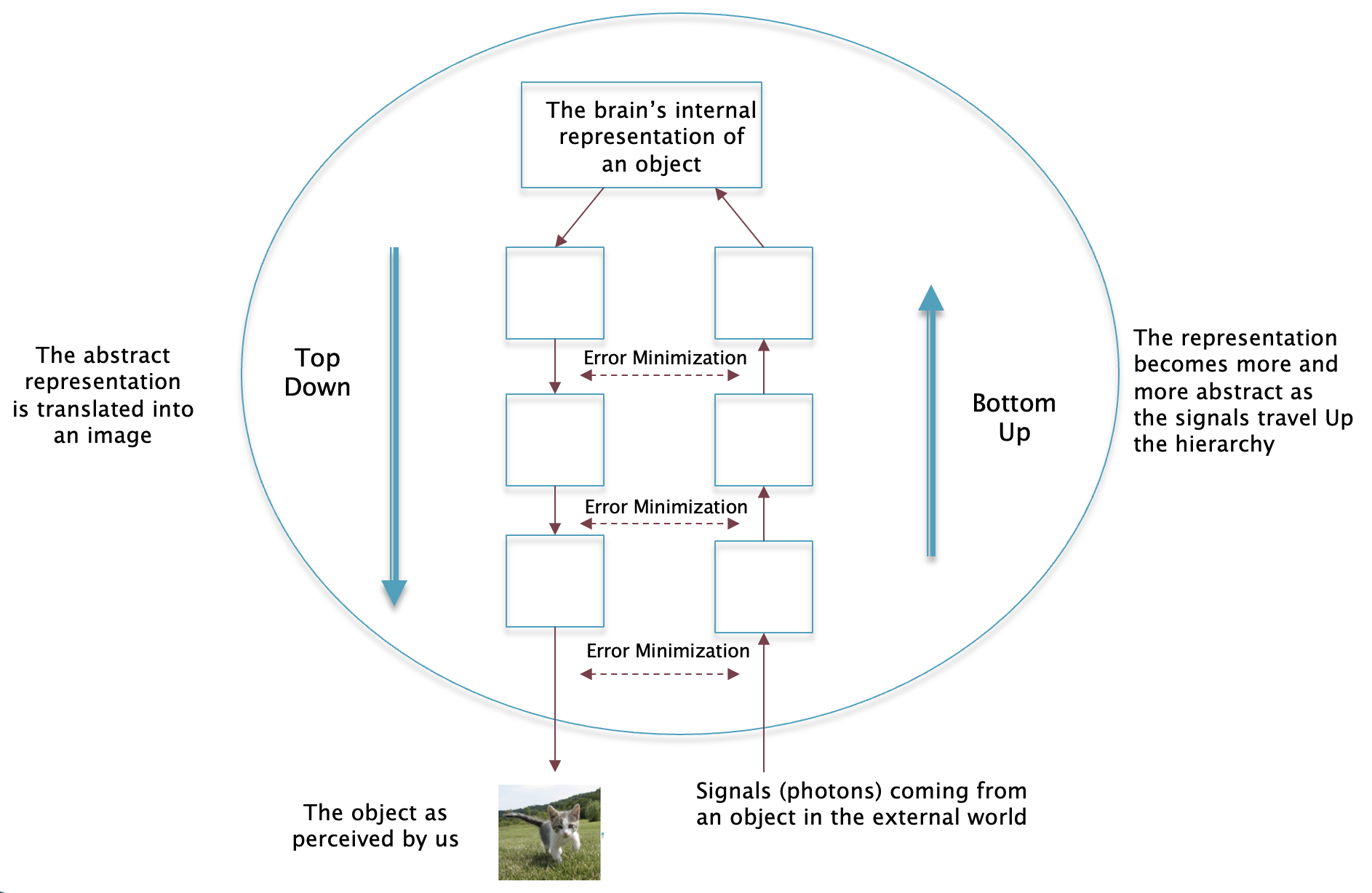
Figure 5
More recently the British cognitive neuroscientist Anil Seth has extended Helmholtz’s ideas by making use what we have learnt about the brain’s operation since then, which is nicely summarized in his book “Being You: The New Science of Consciousness”. His ideas are best captured by the notion of perception as a controlled hallucination (see Fig. 5) and are summarized as follows:
- The brain’s circuitry incorporates generic models for objects that we encounter in our lives. When the circuit is activated, the brain projects an image of the object onto our visual field.
- The brain is also constantly making predictions about the causes of its sensory signals, and these cascade in a top-down manner through the brain’s perceptual hierarchies. These signals themselves stream into the brain bottom-up (or from the outside) and are used to generate prediction errors that register the difference between what the brain expects and what it gets at every level of processing. By adjusting the top-down predictions so as to suppress the prediction errors, the brain’s perceptual best guesses maintain the connection with what is happening in the world. Thus perception happens through a continual process of prediction error minimization.
- Perceptual experience is determined by the content of the top-down predictions and not by the bottom-up sensory signals. Thus we never experience the bottom-up sensory signals themselves (which are nothing more than a count of the number of photons striking the sensory cells of the retina), but only the top-down interpretations of them by our brain.
- The brain does its predictions using the well known Baye’s Rule from probability theory, with the current prediction serving as the prior, the likelihoods encode mappings from potential candidate objects that might have generated the sensory signals. The resulting posterior serves as what actually gets perceived, and also serves as the prior for the next round of predictions. The use of Bayesian ideas here as well as in the QBism interpretation of Quantum Mechanics is interesting.
- If the perceptual priors are very strong, then it results in an actual hallucination. On the other hand when we are paying closer attention to the external world, then the sensory signals dominate, and this results in a picture that is closer to reality.
Anil Seth’s model for visual perception can be considered to be a realization of the idea that Kant originally proposed in the “Critique of Pure Reason”: A way in which the chaos of the noumenal world are organized by the mind and projected into a picture of reality that we see around us. In his book Seth also talks about how other aspects of the mind, such the perception of change, time, moods, emotions and even the perception of the self, can also be explained by his predictive + generative model. He breaks up the hard problem of modeling the mind, into smaller problems of individual aspects of the mind, which can be tied to particular patterns of brain activity.
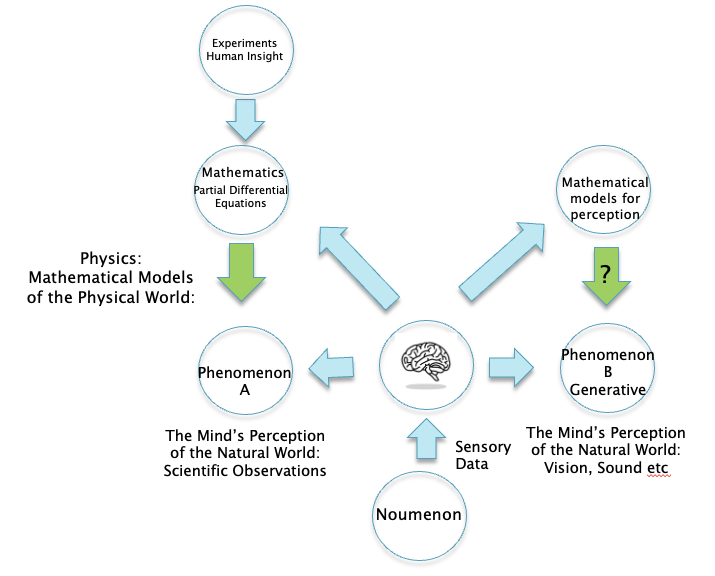
Figure 6
Based on Seth’s work, I have modified the Kantian framework as shown in Fig. 6. I have broken up perceived reality into two types:
- Phenomenon A is what is used in scientific theories. Scientists typically choose a few ‘objective’ quantities from their observations, such as the mass, velocity, electric charge etc which go into their mathematical models. The quantities so chosen depend on the nature of the scientific theory being proposed.
- Phenomenon B is of the type that Seth talks about, i.e., the reality that we see when we open our eyes. The mind uses its own intrinsic models to generate this reality for us. Note that Phenomenon A is a subset of Phenomenon B, and does not capture the richness of our visual perception.
The main purpose for the models of reality that we find in physics, is to make predictions about the future state of the system that is being modeled. Interestingly, Anil Seth’s theory of visual perception is also based on the principle that the brain generates our reality by making predictions. But there is a fundamental difference between the two. The predictions of visual reality made by our brain take place automatically, and we are not even aware that it is doing so. This ability is also presumably something that we share with other animals. On the other hand the predictions made by physics are an uniquely human endeavor and require our capability for logic and mathematics. We are also capable of making longer term predictions that are outside of physics such as: How long will it take me to drive to work today based on the traffic state, or what kind of salary can I expect if I get an advanced degree etc. These point to a capability of our brains to generate future scenarios and do planning based on that, and this may be something that is unique to us.
The Scientific Revolution gave us mathematical models for Phenomenon A. Similarly, is it possible to come up mathematical models for Phenomenon B? In other words, can we mimic the brain’s ability to generate images and other aspects of reality using generative models that are also based on mathematics? This is explored in the rest of this essay.
There is a philosophical school called Phenomenologism that arose in the 20th century, founded by the philosopher Husserl and his student Heidegger. They sought to debunk the idea that by doing physics we are plumbing the depths of reality, since the equations of physics are two levels removed from the base reality: Level 1 being the abstraction created by our minds, and Level 2 being the further abstraction whereby certain aspects of our perceived reality are chosen to be part of models used in the equations of physics. Hence our subjective experiences are infinitely more complex than any physical theory can capture, and we can never hope to describe all of it using mathematics. For an accessible overview of recent developments in this philosophy see the book “The Blind Spot: Why Science Cannot Ignore Human Experience” by Frank, Gleiser and Thompson. This point of view is in agreement with the framework shown in Fig. 6.
What about models for consciousness? Seth thinks that generative models of the brain can ultimately be extended to explain consciousness as well. Note that the Kantian framework says that just as perceived reality is a creation of brain, at the same time the brain is one of the objects that exists in this reality. This circular path is often referred to as a “Strange Loop” in Cognitive Science. There are some philosophers and scientists who believe that it is impossible to come up with models for consciousness and the experience of qualia, since these are being generated by the ‘real’ brain that exists in the noumenon, to which we have no access. The brain that we see in the phenomenon is not the same thing as its noumenon version, and as a result the “Hard Problem of Consciousness” cannot be solved using the data that we have. Please the book The Case Against Reality by Donald Hoffman for a good explanation for the point of view that consciousness cannot be explained using models of the brain. In this essay we will restrict ourselves to models for visual perception and language, which are also hard problems, but not as hard as that of consciousness.
Mathematical Models for the Mind
In the previous section we described a Kantian framework for science that proposes that since the brain is one of the objects that exists in our perceived reality, we should be to model it using the Scientific Method, and aspects of the mind should arise from such a model. The brain is a special case, since we use it for creating reality, and hence in a sense the brain is trying to model itself within the confines of the perceptual boundaries that it has created. In the prior section we described Anil Seth’s “Controlled Hallucination” theory of the mind which operates within the Kantian framework and provides mechanisms by which specific aspects of the mind emerge. In this section and the in the succeeding two, we will look at how ANN models exhibit properties that are similar to that of the mind, in particular we will look at mathematical models for visual perception and language.
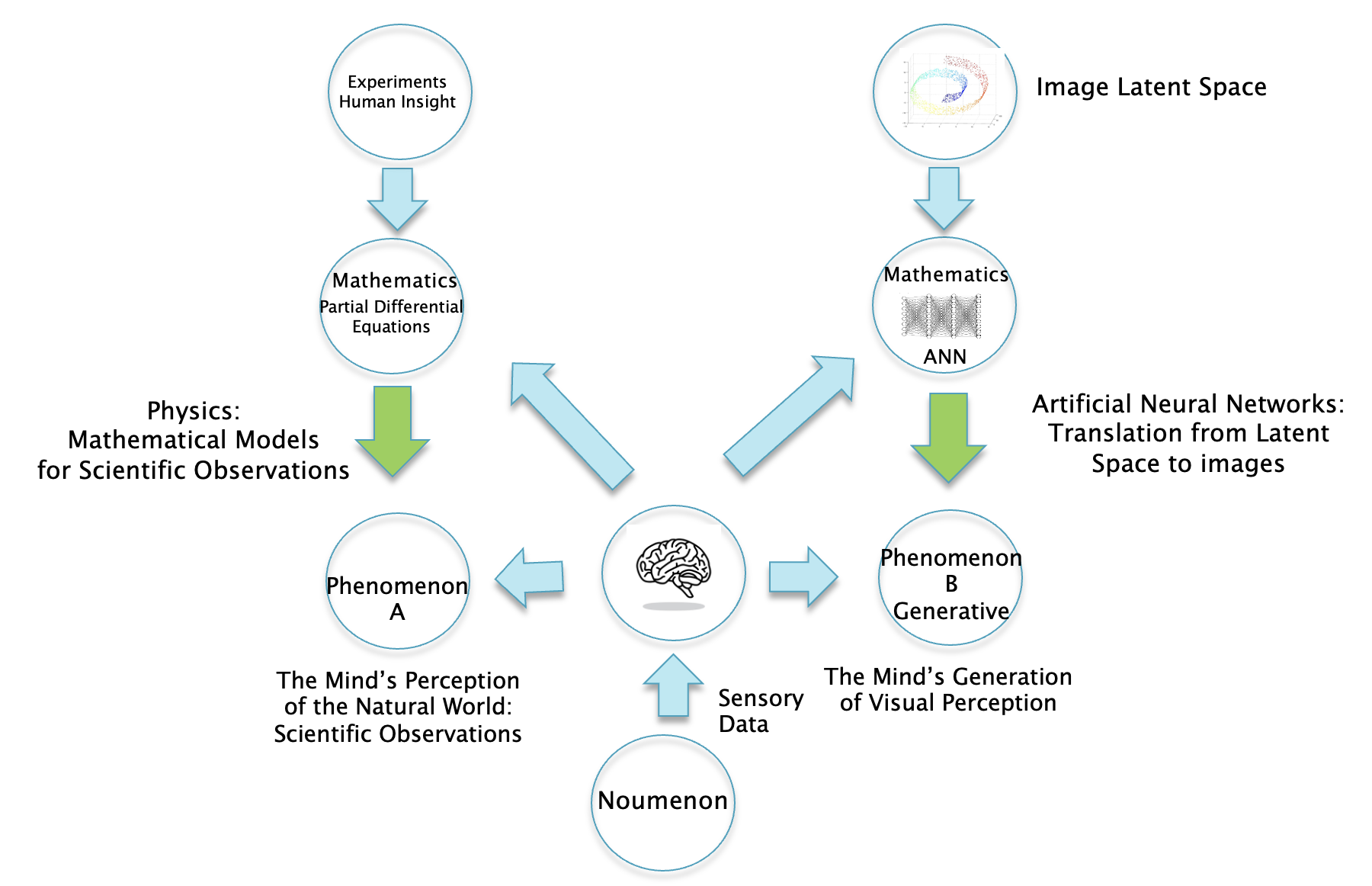
Figure 7
Fig. 7 proposes that mathematical models for the brain take the form of Artificial Neural Networks (ANNs). These models are different than Partial Differential Equations (PDEs) that are used in physics and point to a fundamentally different way for building mathematical models of reality. How are they different?
-
Models for scientific observations (on the LHS of Fig. 7): These take the form of PDEs and are created by scientists by focusing on aspects of reality that can be measured using instruments. The process by which they are able to “guess” the right equations remains a mystery of human creativity, but some of the things they rely on includes prior work by other scientists, experimental results, mathematical theories and lastly and most importantly their own intuition. Even though models for physical reality make use of advanced mathematics, at their root they are simple, in the sense that they are able to model complex physical phenomena using only a few equations with tens of parameters. It can be argued that the reason why this is even possible is because of the a priori structure that our minds create in order to organize the chaos of data coming from the noumenon. According to Kant these structures include our perceptions of space and time, and these simplify these models of quite a bit, since these imply that all interaction between entities in the model is limited to entities that are in the (space-time) neighborhood of each other. Without this simplifying assumption building mathematical models of physical reality would be impossible.
-
Models for visual perception (on the RHS of Fig. 7): These take the form of ANNs that can have billions of (artificial) neurons interacting with each other. Unlike our mind, ANNs don’t come with any simplifying a priori structures like space and time which have been built up over hundreds of millions of years of evolution. Indeed, ANNs consist of models in which individual neurons can potentially interact with all other neurons in the model, which makes these models extremely complex. Consequently we also need billions of parameters to model all these interactions, so these models are very different than the parameter sparse PDE models. It is impossible to obtain these parameters using experimentation, and instead they are estimated using a process called training. During training, we try to match the input into the model with its known correct output, and if they don’t match then we modify the model parameters slightly using an algorithm called Stochastic Gradient Descent. This process is repeated hundreds of millions of times until the two get sufficiently close to each other. There is no logical justification for the resulting parameter values other than the fact that they lead to ‘correct’ outputs given an input, so the model is not comprehensible in the sense of models in physics, it is a Black Box. Before training starts, the “mind” of the ANN can be considered to be a Tabula Rasa or a blank slate since all their parameters are set to random values (strictly speaking we do endow the ANN with a pre-existing connection topology, so it is not entirely a Tabula Rasa). Which is why it takes so much a data to train the ANN, in some sense we are trying to reproduce the gradual process of natural evolution in biological brains within a few days of training. During this time the ANN must discover the structure of the world through the images and text that we feed into it.
In some sense the pixel level data in the input images can be considered the be the equivalent of the noumenon for ANNs. Just as our mind organizes the chaos of the actual noumenon using structures as space and time, similarly ANNs must use some organizing principle to structure the chaos of pixel data that we feed into them. As a result of the training, the ANN parameter values are no longer random, but assume values that enable it to recognize patterns that are present in the data. When a pre-trained ANN is subject to new data that is not part of the training set, this is analogous to fresh sensory data coming into our brain. Due to its training, the ANN is now able to extract meaning from the data and carry out tasks that are useful to us.
How do ANN Models for Visual Perception Work?
Just as the brain organizes the chaotic light and sound data coming from the noumenon into our orderly perception of the world, ANN models for vision are able to organize the pixels, which are just blobs of color, into images that make sense to us. How do they do this? Anil Seth’s work is an example of a theory that explains how visual perception works in our minds. It involves a number of different mechanisms, the main ones being the ability to generate images of objects from information that is already in our minds and the ability to predict the next ‘frame’ of the visual perception. We will first focus on the generation part and see how ANNs are able to do this.
The generative capability of ANNs was discovered in the early days of Deep Learning when ANN models were mostly used for image classification, which was done by feeding image pixels into a model, with the output of the model corresponding to the probability distribution over the various image categories. Researchers found out that when this model was run backwards, i.e., if the output corresponding to a particular object category was stimulated, then the pixels coming out at the other end actually looked like the object! It didn’t look exactly like the images that were fed into the ANN during the training process, but one could see that they were derived from them. When I was first learning about ANNs, I remember being fascinated by this property, and it fed my subsequent interest in these systems. The fact that the ANN was able to reproduce images of objects meant that it was not merely learning enough information from the training data to classify images, but it was learning higher level information about the object that was sufficient for it to be able to reproduce its likeness. Since those very early examples of image generation, the state of the art has progressed quite a bit, with the latest models such as OpenAI’s DALLE-3 or Google’s Gemini being able to generate photo realistic images in high definition.
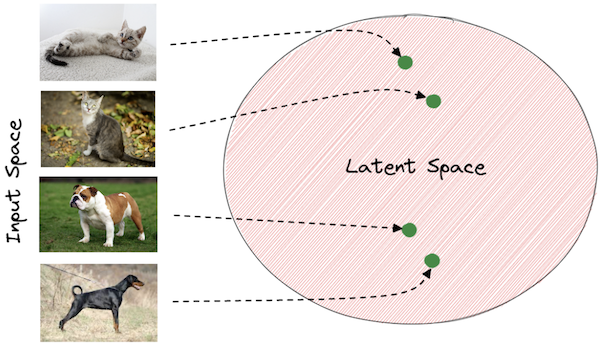
Figure 8
The simplest way to understand how ANNs generate images is to think of it as a mapping from the space of image pixels, to a higher level representation called a Latent Vector (which is just a bunch of numbers organized in one or two dimensions). A Latent Vector captures the information in the image, but in a highly compressed form. Images have a lot structure in them, which leads to redundancies in the way they are expressed using pixels. The ANN strips away all these redundancies and is able to capture the patterns in the image using just a few numbers, and these are summarized in the form of the Latent Vector. These vectors exist in a higher dimensional space called Latent Space, and every image maps to one of the vectors in this space. The Latent Space is a fantastically complex mathematical object that exists in a space with hundreds of dimensions, to which we had no access to before the advent of ANNs. It has the nice property that if we interpolate between the Latent Vectors for two images, then all the vectors lying on the linear segment connecting the two also correspond to valid images (such an object is called a manifold in Differential Geometry). Hence the ANN maps image pixels to points in the image manifold, and it generates images by reversing this operation, as explained next.
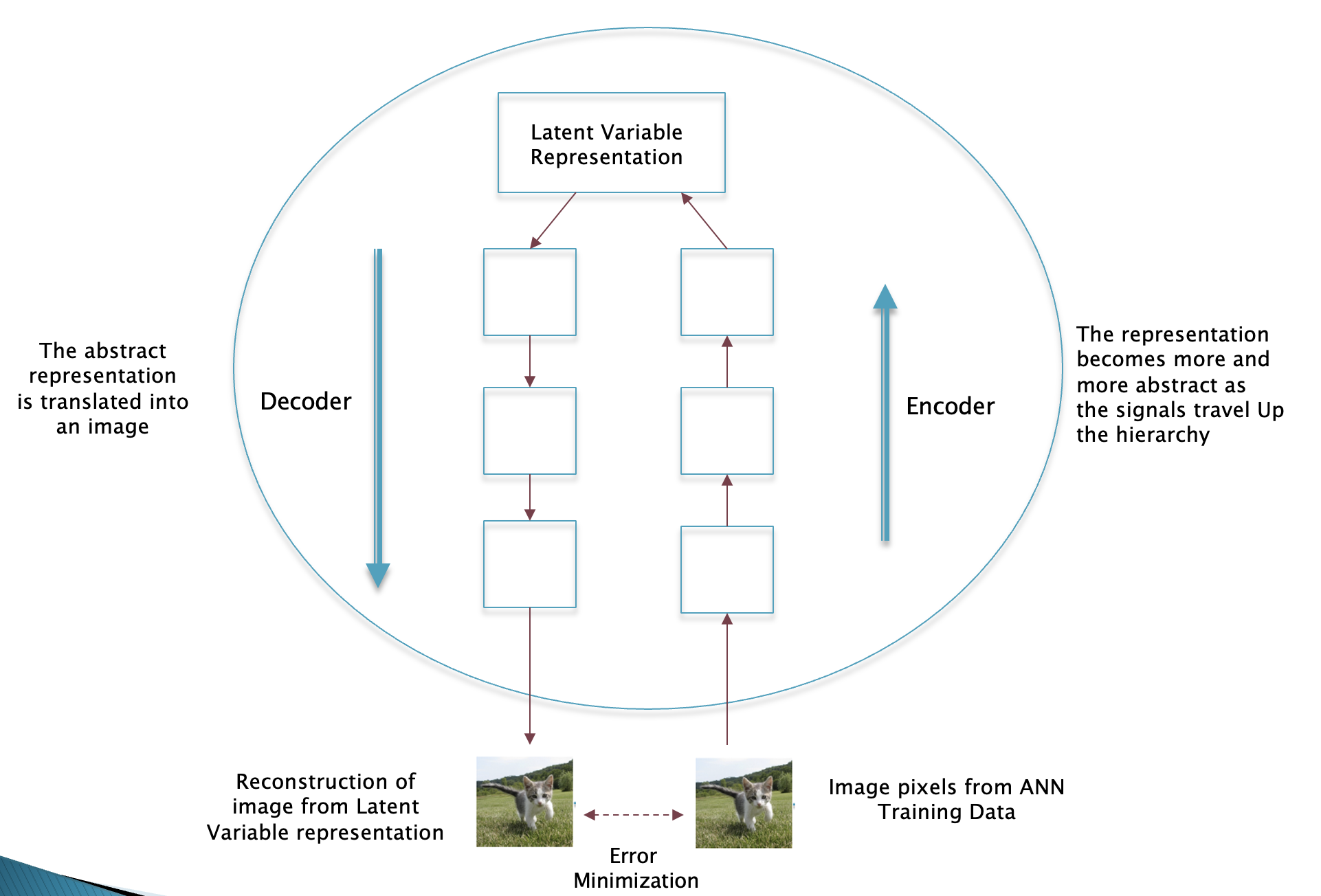
Figure 9
The general principle for training an ANN to generate images is shown in Fig. 9, and you may notice that it is quite similar to the Anil Seth’s model for visual perception. There are two operations encoding and decoding. The encoding operation (shown in the RHS path in Fig. 9) can be likened to processing the chaotic information coming in the form of pixels, and this is done in an hierarchical fashion, which ultimately results in the creation of a Latent Vector corresponding to the image. The decoding process involves turning a Latent Vector back into pixels, as is shown in the path on the LHS of Fig. 9. This involves taking the bare bones representation of the image in the Latent Vector form and gradually adding the shapes and textures into it until it becomes a fully formed image. The error between the input and its re-constructed version is then used as a signal to change the model parameters so that the agreement improves. Different ANN models use different techniques to implement the encoding and decoding pipelines, and currently the best system that we have are called Diffusion Models.
The brain is a much more complex system than ANNs, given that each neuron can have thousands of dendrites connecting it to other neurons, and it is not fully understood how it is able to perform the encoding and decoding operations. We do have some idea of how the brain does encoding, and this was discovered in the 1960s in a series of famous experiments carried by David Hubel and Torsten Wiesel. In fact, the ANN called Convolutional Neural Network was subsequently designed to mimic what we had learnt about the brain from these experiments. The generation process in the brain is much more complex than simply inverting a Latent Vector and involves inputs from a large number of brain regions and is not as well understood. The neurons in our brains do a much better job of modeling the external world, given that we are able to model new objects from just a few examples that come into our field of vision, whereas much more data is required for training an ANN. It is quite likely that the ability to this is one of the a priori capabilities that has been built in our brains over hundreds of millions of years of biological evolution.
So far we have discussed the ability of ANNs to generate images, but this is not enough. You may recall from Anil Seth’s theory that our brains exhibit the ability to not jest generate images but are also able to predict the next ‘frame’ of our visual perception. Can ANNs do that? It turns out that the generative models that are used to create images can be extended so that they can generate short video clips. As for images, video clips can be mapped on to a Latent Vector, and vectors from this space can be decoded to generate new clips. These clips thus generated are of high quality, but they often betray ignorance of reality, such as a glass object bouncing when dropped on the floor instead of shattering. Hence there is more work required before we can use ANNs to generate feature length movies, but fast quick progress is being made in this area.
This brings us to the next element Seth’s model for visual perception, which is the ability for the generation process to continually self-correct based on the information coming in from the sensory organs. Clearly with the current state of technology, ANNs cannot do this, the following hurdles stand in the way: The brain is constantly updating it model of reality, based on the information it is getting at every instant. This process starts when we first open our eyes, to the time that we die. As a result of this, its model of reality become more accurate over time, and any disagreements are gradually trained away. In order to do this, it is required that the agent (i.e. humans) carry the model around in their heads. This is clearly not the case for the most advanced ANNs that exist currently. They require huge datacenters with lots of GPUs and memory and have also have massive power requirements. Hence the way things work today, they are trained once using a large dataset, and after this all their predictions are based on the model that developed during the training process. Hence their world model is static, while ours is dynamic since it is constantly getting updated. In order to get closer to the brain, ANNs should be able to constantly re-train themselves based on current data. Obviously this cannot be done if the ANN is housed in a data center, and there are two ways in which we can solve this problem: (1) Allow the ANN to go out into the world, as part of a robot. This clearly will not work with the current server based paradigm, (2) Attach a camera and microphone to a human who is constantly feeding this information back to the ANN (this is a bit like the training that self driving cars do, where they drive on city roads for several years to improve their model).
Why is it important for the ANN to be able to make good predictions of reality? Other than the fact that it enables us to generate video clips that look like the real world, this ability is critical in doing planning. We will talk more about in the following sections, but here is a preview: Planning is the ability to be able to run future scenarios ‘in our head’, so that we can figure out the best way of accomplishing a task. In this situation the generated images are no longer being corrected by real time data, which makes it important to get the predictions right. If the ANNs ability to do this is suspect, then this will clearly impede it ability to do planning.
Language within the Kantian Framework
So now we finally come to the topic that was advertised in the title of the essay, namely LLMs and human language. Just like visual perception, mathematics, science and ANNs, language is a creation of the human mind. It is a very old creation, it is estimated that human language arose about 50,000 years ago, and it also coincided with a leap in human cognition that happened around the same time. Philosophers did not turn their attention towards language until the 20th century, and the name that stands out is that of Ludwig Wittgenstein. He came up with a theory of language in his work Tractatus Logico-Philosophicus which was published in 1918.
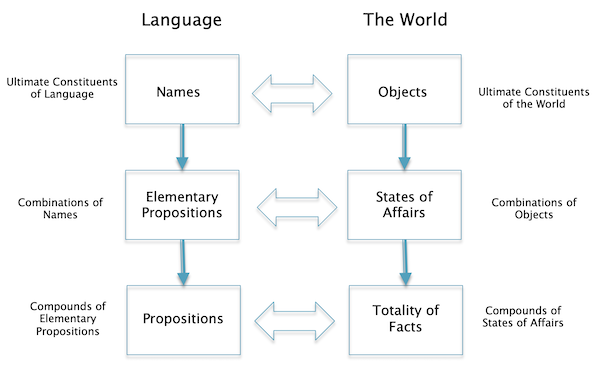
Figure 10
The main aspects of Wittgenstein’s theory of language are summarized below (and also shown in Fig. 10). This description is taken from the excellent book The History of Philosophy by A.C. Grayling.
- Both language and the world have structure.
- Language consists of propositions, which are compounds of ‘elementary propositions’, which in turn are combinations of ‘names. Names are the ultimate constituents of language.
- The world consists of the totality of facts, which are compounded out of ‘states of affairs’, which in turn are combinations of ‘objects’.
- Each level of structure in the world is matched by a level of structure in language: Names denote objects, combinations of names constitute elementary propositions that correspond to state of affairs, and each of these in their turn combine to form, respectively propositions and facts.
- The arrangement of names at the most fundamental level of language structure ‘mirrors’ or ‘pictures’ the arrangement of objects at the most fundamental level of the world’s structure. This called the ‘picture theory of meaning’ and is central to the philosophy.
- Thoughts are what can be expressed using language and are propositions in that language. They are only true if they can be translated into a picture. Only propositions in science satisfy this requirement. The propositions in mathematics (which is also a type of language) are tautologies, i.e., they are always true regardless of the state of the world.
- Propositions in religion, philosophy, ethics, aesthetics etc, cannot be expressed in words (that satisfy the criteria for a true proposition). For these, ‘showing’ rather than ‘saying’ is all that is possible. They are not pictures of actual or possible facts, and therefore are meaningless. This however does not mean that they are un-important, Wittgenstein though that they are the truly important parts of human knowledge, it’s just that we cannot talk about them to figure out whether they are true or false (he put his own work into this category).
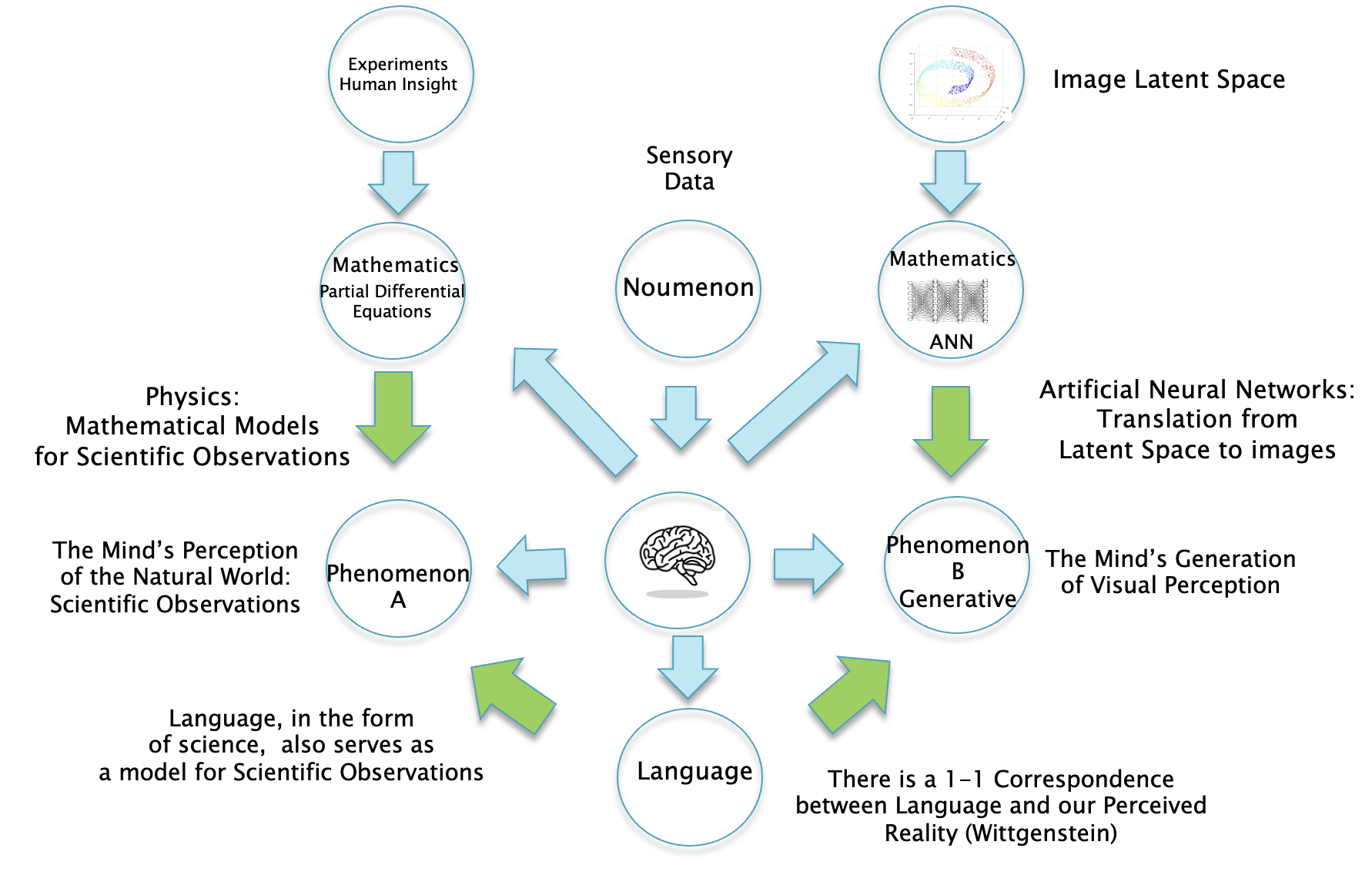
Figure 11
Fig. 11 shows a way in which we can fit language within the Kantian Framework. It captures the fact that language is another creation of the brain, and also Wittgenstein’s ideas of the relationship between language and visual perception, as well as the idea that language captures the propositions of science. Hence in some sense language is the most powerful creation of the mind, since it encompasses other aspects of generated reality as well our ability to do science and mathematics.
ANN Models for Language
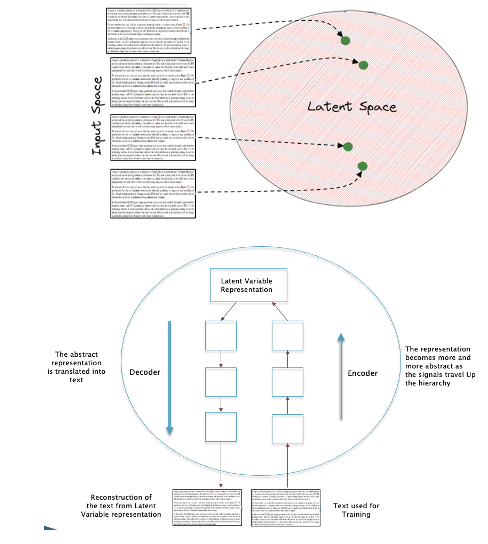
Figure 12
ANN models for language, called LLMs, proceed along the same lines as those for vision, with the main difference being that image pixels are now replaced by individual words (there are LLMs that can be built by directly using characters instead, and those work almost as well). As shown in the top part of Fig. 12, LLMs map pieces of text to points in the language Latent Space. Just as for images, language has a lot of structure in the relationship between words, and ANNs are able to capture this structure and thereby reduce the representation of a piece of text into a highly compressed form involving just a few numbers. As for images, these Latent Vectors live in a high dimensional Latent Space, such that each point in this Latent Space corresponds to a piece of text. The discovery of the language Latent Space, along with the means to decode from it, seems to have settled a long standing open problem in Artificial Intelligence of how to generate language which sounds like it came from a human (also known as the Turing Test).
There are two aspects of the science of language (called Linguistics), namely syntax and semantics. Syntax denotes the rules which capture the Grammer in language while semantics captures the meaning. There were logical models for syntax before the advent of ANNs, but nobody had been able to find a mathematical model that captures semantics. The Latent Space for language seems to be one such model, and given the complexity of the mathematical structure within which it exists, it explains why it hadn’t been discovered before the advent of LLMs. Interestingly enough, the same ANN model, namely Transformers, has been used to build models for both image and language, which points to an underlying similarity in the structure that underlies them. We explore this relationship in the following section.
The bottom part of Fig. 12 shows the process by which LLMs are trained. The text from the training dataset is fed into the LLM, which then converts it into a vector in Latent Space. This vector is then decoded to regenerate the original text, and the difference between the reproduced text and the original text is used as an error signal to train the model. In practice the text is input into the model on a word by word basis, and the output text is also produced likewise word by word. LLMs are trained using huge datasets that encompasses most of the language that can be found in books and online.
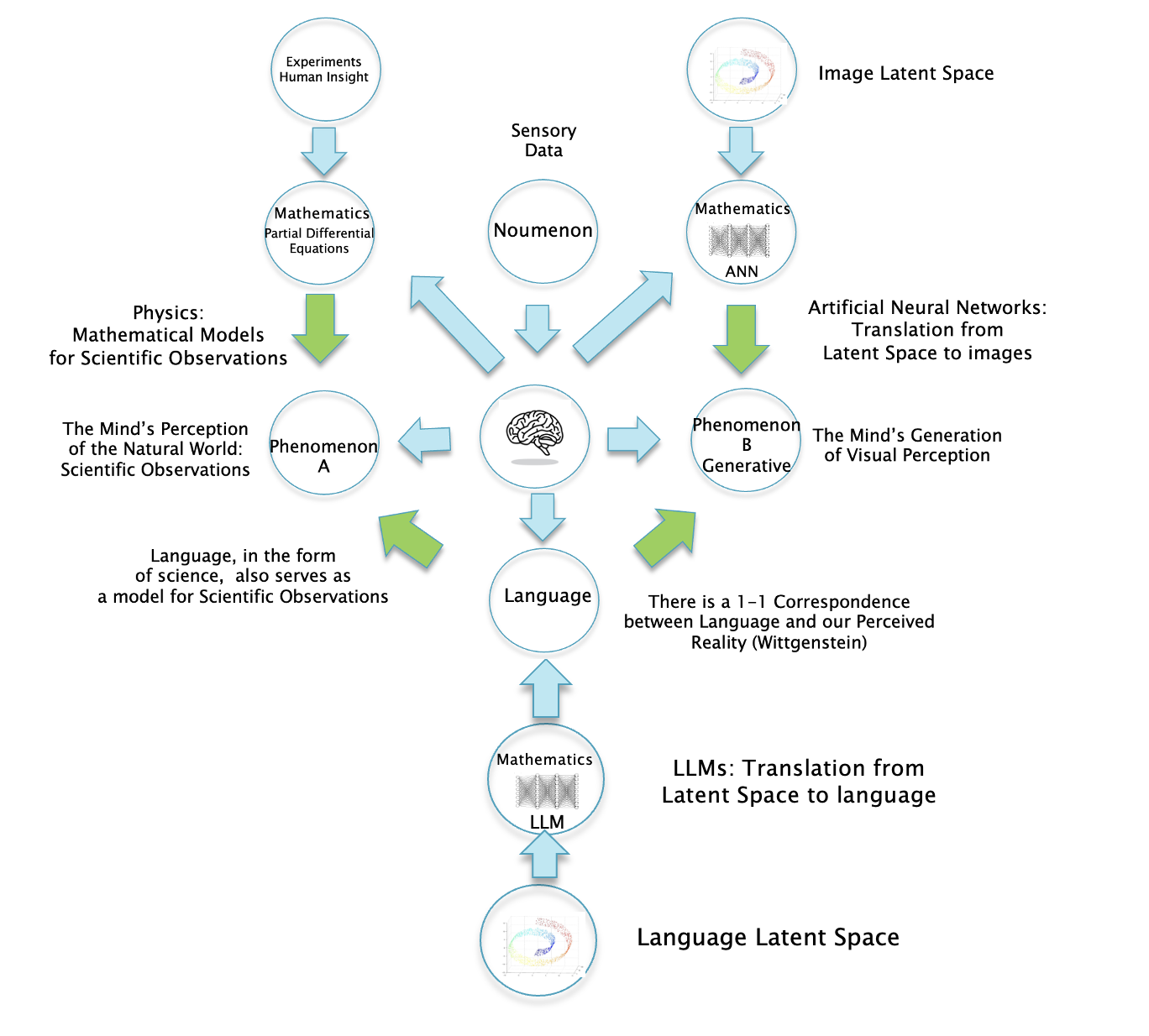
Figure 13
Fig. 13 shows the LLM as integrated within the Kantian framework. It shows that both LLMs and Image ANNs serve as mathematical mappings from the language and image Latent Spaces respectively, to actual text and images.
Language is an all purpose technology that we humans have invented that enable us to communicate and as Wittgenstein pointed, it also serves as a model for the world. Moreover the language of science (and mathematics) is encompassed within this. This raises the interesting question: Since LLMs serve as a mathematical model for language, do LLMs inherit language’s ability to model the world and also be able to generate scientific knowledge? We will examine these questions in the following sections, starting with the connection between language and images as revealed to us by ANNs.
A Wittgenstinian Connection Between ANN Gnerated Images and Text
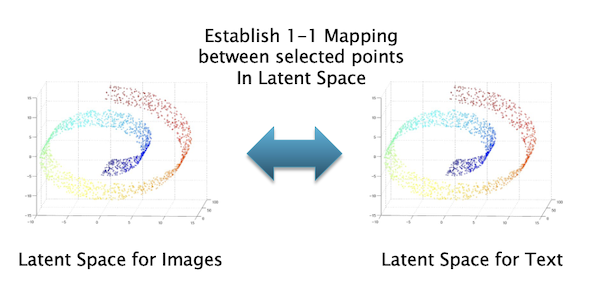
Figure 14
Wittgenstein hypothesized that the propositions of language correspond to pictures in the world. It turns out there is an exact mathematical isomorphism (or one-to-one correspondence) between ANN generated text and images and this exists at the Latent Space level (see Fig. 14). This deep relationship between these two domains was not discovered until recently, because we didn’t have access to Latent Space before ANNs were invented.
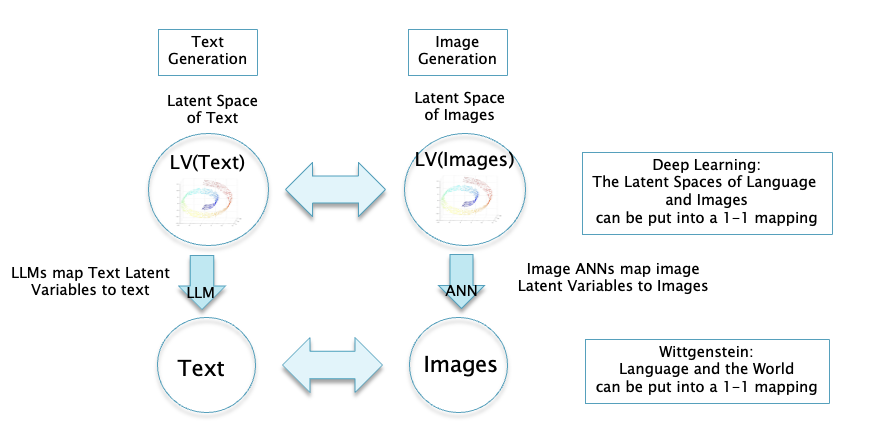
Figure 15
We can start with a Latent Vector in the language Latent Space and convert it into a piece of text using an LLM. Alternatively we can take the Latent Vector in the image Latent Space that corresponds to the text Latent Vector, and convert it into an image using an image generator ANN. We will find that the semantic content of both the generated text and the image are the same. Hence the isomorphism between language and images is laid bare at the level of their Latent Spaces.
There are two ways in which the correspondence between text and images Latent Spaces can be established during the ANN training process:
- A piece of text is converted into its Latent Vector representation, and the same is done for the image that it is a caption for. Then the LLM and the ANN models are fine tuned so that the distance between the Latent Vectors for the text and its corresponding image move closer to each other in Latent Space (in reality a slightly more complex algorithm called CLIP is used). This was the technique used in the DALLE-2 image generator from OpenAI.
- A piece of text is converted into its Latent Vector representation, and the very same Latent Vector is used to generating the corresponding image. The difference between the generated image and the training image is then used to train the image generator model (which is a diffusion model). This technique is used in the latest generation of Image Generators including DALLE-3, Gemini and Stable Diffusion.
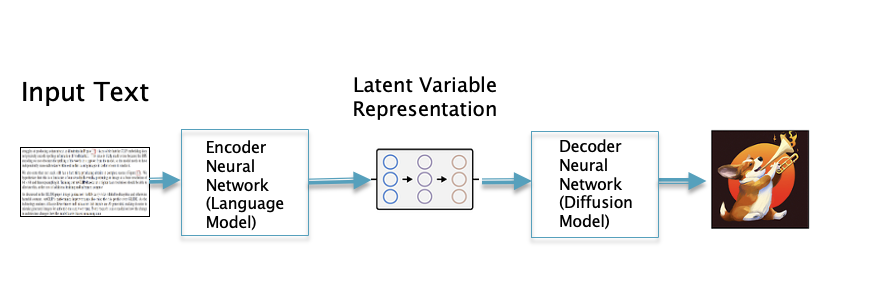
Figure 16
If we use the second technique described above, then we can start with a piece of text and convert it into a Latent Vector in the language Latent Space using an LLM. We can then use the very same Latent Vector to generate the corresponding image (see Fig. 16).
I still find this discovery that language and images can the mathematically reduced to the same set of numbers fascinating, and I don’t think we have realized all the implications of this. The training process basically minimizes the distance between the text and image Latent Vectors for the training dataset. This admittedly is a large sample, but it is still less than all possible text-image pairs that can exist. The fact that establishing the correspondence for a subset of all possible samples nevertheless leads to an isomorphism between ALL possible samples, means that the topological structure of the language and image Latent Spaces are identical. Does this property hold for the brain as well? If so, it means that the brain circuitry that was developed for vision over hundreds of millions of years has been re-purposed for language. This also means that other higher animals have probably developed the ability to communicate using language. Indeed ANNs are being used in several studies to denote the complex click soumda that whales and dolphins make.
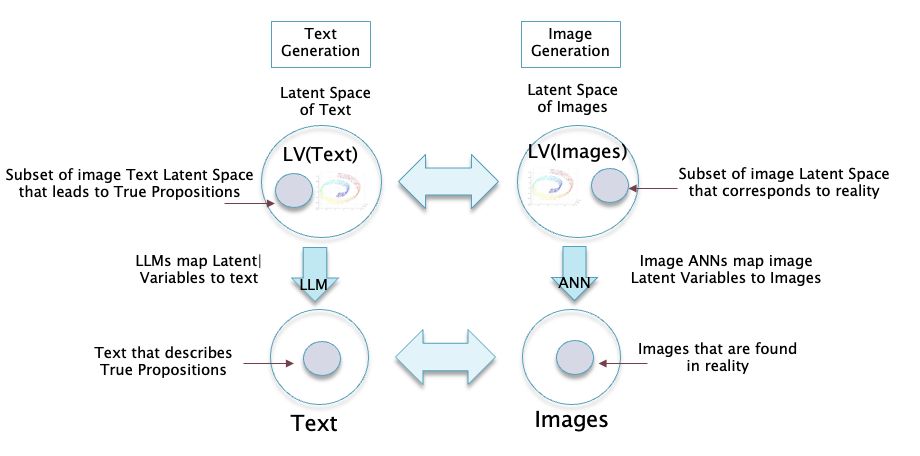
Figure 17
Not all text corresponds to facts in the real world, the subset that does were called True Propositions by Wittgenstein. True Propositions map isomorphically to the subset of images that correspond to reality. Similarly, there are subsets of the language Latent Space and the Image Latent Space that correspond to True Propositions and to reality respectively, and they also map isomorphically to each other (this is shown in Fig. 17).
How can a LLM tell whether a vector in its text Latent Space translates into a True Proposition? It cannot, this is something only a human can do since only humans are in direct contact with reality (this is the well known problem of hallucinations in LLMs). The world that is described to the LLM during its training consists of text taken from the open Internet and from books, and some of these may not be true. If an LLM cannot differentiate between True and False Propositions, then how can it be used to do science? We will investigate this question in the following section.
Can LLMs Do Mathematics or Science?
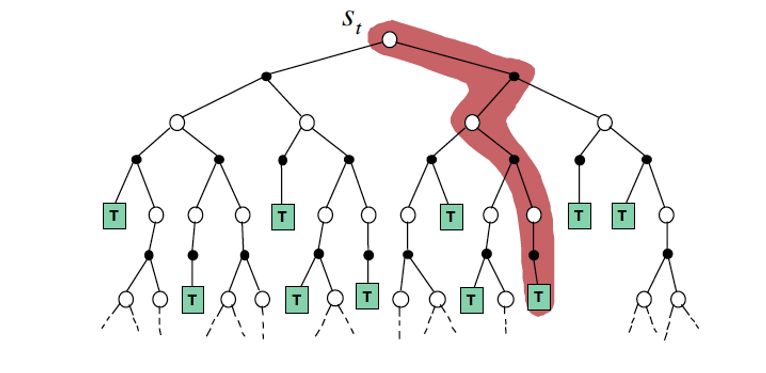
Figure 18
There is a difference between the kind of thinking our brain engages in when it is doing mathematics or science (which is the process shown on the LHS of Fig. 13), vs the kind of thinking involved in generating images or language. This is the same distinction that was made by the psychologists Kahneman and Tversky, who referred to the latter as System 1 thinking and to the former as System 2 thinking. System 1 thinking is intuitive and automatic, we are not even aware the work that the brain does to generate the reality we see, or come up with a grammatically and syntactically correct statement. System 2 thinking on the other hand involves conscious effort on our part and is probably unique to humans. This is the kind of thinking we do when we are doing mathematics or science, playing a board game or even doing planning in our daily lives (such as how to organize a vacation).
System 2 thinking can be captured by the decision tree graph shown in Fig. 18, which is of the type used in a subfield of Artificial Intelligence called Reinforcement Learning (RL). Fundamental to RL is the idea of an Agent, which in this case is our brain. There are two kinds of nodes in the graph: The white nodes correspond to States of the world, while the black nodes correspond to Actions that an Agent might take. For example when we are driving a car, the Actions correspond to movements of the steering wheel or the brakes, while State corresponds to the changing view of the world that we see. Alternatively when we are trying to solve a math problem, the State is the current state of our calculation (assuming it involves several steps), while the Action corresponds to mathematical operations that act upon the State. The decision tree captures the fact that the solution of a System 2 type problem involves choosing among several alternative Actions at each step, and the Agent has to navigate the decision tree in a way so as to successfully complete the task.
System 2 thinking can be accompanied either by taking Actions in the real world to achieve some objective (for example drive to work), or alternatively it can be carried out entirely in our head. The latter mode of thinking in which we trying to figure out how to accomplish a task without actually taking any real Actions, is called planning, and it is done in two contexts:
-
Solving a problem in mathematics: Solving a math problem does not involve any interaction with the world, and is entirely an abstract exercise. Wittgenstein pointed out that the propositions of mathematics are tautologies, i.e., they are always True irrespective of the state of the world. Mathematics does not have anything to do with reality, mathematical systems are built using logic, and as long as there are no errors in the logical process, the resulting propositions are correct.
-
Solving a problem that involves knowledge of the world: Consider the example of trying to assemble a piece of furniture using instructions that came with it. The actual assembly process involves taking Actions in the real world, but assume that before the assembly starts we mentally try figuring out the various steps involved. The latter is an example of planning, and in order to carry it out, we need to create a mental picture of how the furniture would look as we carry out each assembly step. These mental pictures would then correspond to the State of the assembly decision tree. From this example we can see that in order to carry out a System 2 planning task planning successfully, our mind needs to give us an accurate picture of the reality (or State) that would result if we were to carry out an Action.
Can we replace our mind with an ANN and still be able to solve System 2 type problems that involve planning? In order for an ANN to successfully do System 2 planning, it needs to be able to reliably predict the next State, given an Action and the current State in the decision tree. In order to do this, the LLM needs an accurate model of the world which tell it how things change as it navigates the decision tree. Hence if we can’t be sure of its Next State prediction abilities due to hallucinations, then it won’t be very useful in this regard.
If the ANN is embodied in a robot, it is constantly receiving feedback about its Actions from the camera and other sensors it has, so it would seem that it can potentially solve a System 2 problem without any ability to predict the next State, i.e., without doing any planning. However if we think more deeply about this, before the robot can take an Action, it has to figure out how that Action might affect the State of the world. Hence even in this case the Next State prediction ability is critical. In order to be successful, the robot has to plan out the sequence of Actions that will increase the chance that it accomplishes its task, and this has to be done before it takes any Action in the real world.
Another important skill needed in navigating the decision tree is the ability to prune it down to a manageable size, and this skill is needed whether we are acting in the real world or doing planning. This issue arises since potentially one can take a huge number of Actions at any stage in the tree, which means the tree size can quickly balloon to a huge number of nodes. However our minds have the ability to intuitively pair down the number of Action choices to a manageable number and this is a critical skill that is needed whether we are solving a math problem or planning a vacation. This ability is key to intelligent behavior, and in the human realm it distinguishes the most skillful people from the rest of us. Do ANNs have the ability to prune decision trees? It turns out that this ability is actually a System 1 skill, even though it being performed within the context of a System 2 task. In other words the ability to figure which course of Action to take is something that we do intuitively and sometimes without knowing why we made a particular choice. Since ANNs are good at performing System 1 tasks, it stands to reason that they should be able to prune decision trees quite well too. One of the smartest ANN systems is the one called AlphaZero that was designed by DeepMind to play Go, Chess and other board games. AlphaZero consists of a decision tree that is trained using Reinforcement Learning, and an ANN, whose main function is to prune the decision tree. In the case of games, the world model is relatively simple since it is confined to the board, however similar designs are being pursued to do planning using ANNs in real world contexts too. My blog LLM Based Autonomous Agents digs deeper into this area.
The best scientists among us have an extreme ability in the decision tree pruning area. Indeed Einstein was able to deduce the Theory Special Relativity from the single fact that the speed of light is an universal constant and the General Theory from the Equivalence Principle. It is unlikely that ANNs will get to this level anytime soon, however ANNs do have another scientific ability that will turn out to be as useful: This is the ability to recognize patterns in a mass of data, which are not visible to humans. The ability to form a model for language is a good example of this skill. There are problems in physics, and even more so in other sciences such as biology or economics, where there is a lot of input-output data, but no simple formula that connects the two. However, ANNs are capable of coming up with a mathematical model for these cases, the only difference is that now the model is not in the form of a few elegant equations, but is captured in the hundreds of millions of parameters of the ANN. Mathematics at the most advanced level also involves decision tree pruning, especially in trying to dream up new mathematical structures with interesting properties. For a deeper dive on this subject see my blog Artificial Neural Networks and the Scientific Method.
From discussion so far we can conclude the following:
- ANNs can be used to solve mathematical problems since it does not involve any interaction with the world. As long as the ANN has the ability to reason correctly, not make logical mistakes and also be able to prune down the decision tree, it can be very good at math. Indeed LLMs are getting better at these skills and have achieved impressively high scores in college level datasets such as MATH.
- ANNs cannot be used to solve planning problems that involve acurate predictions of the next State, since with the current state of the art, the ANN has no means of knowing whether the next State it is generating corresponds to reality or not. Problems in physics or even the solution of planning problems we encounter in our daily lives belong to this class.
In more restrcited environments such as when the ANN Agent is playing a board game, the state of the world corresponds to the current configuration of the pieces on the board, hence is a much simpler system to model and do predictions on. Please see my blog LLM Based Autonomous Agents for examples in which ANNs were shown to have developed accurate world models for the games of Chess and Othello.
How is it that humans have a more accurate model of the world as compared to ANNs? There are two main reasons:
- The world model in humans is developed during the course of childhood and growing up into an adult (in addition to some a priori concepts that come pre-loaded into our brains, as Kant pointed out). During this time our training data comes directly from the world around us which allows our world model to become more and more accurate over time. On the other hand, ANNs are trained using data (which can be video, images or language) which may or may not correspond to reality which makes it more difficult for them to obtain an accurate world model.
- The human world model is being constantly updated during our waking hours, all throughout our lives. This is done using the process that Anil Seth has proposed, whereby our brain is constantly generating predictions using it current model, and these are verified against the data that is coming through our senses. If there is a difference between the two, then our internal model is modified in order to get a better prediction. ANNs on the other hand don’t have any kind of interaction with the real world. Once they get trained, then all their predictions are generated by their stored model, and they have no opportunity to make improvements.
What can we do to improve ANN performance for class 2 planning problems involving real world predictions? There are potentially two ways:
- Make sure that the training data only consists of samples that reflect reality, i.e., confine it to the smaller subset shown in Fig. 17. However, this is not the ideal solution since the world is a dynamic place, hence the world model that the ANN learns today will be outdated by tomorrow.
- Use an architecture similar to the one that Anil Seth proposed for the brain, i.e., even after the initial training is complete, constantly check the next state predictions with the new data that is coming in, and use the difference to fine tune the ANN.
The latter way requires that the ANN be localized to the Agent, which could be a robot, and thus the fine tuning will be customized to the sensory data coming to that particular Agent. This is not feasible today since the most advanced models require huge amounts of compute and memory that is only feasible in the Cloud (unless the provider partitions the available compute resources into individual chunks, similar to the VM concept). The fine tuning will take time since it will be a gradual process as the Agent acts out in the real world and gathers more data. Hence the process of improving the Agent’s world model becomes a longer term proposition. Hence in some sense Seth’s model for the brain is a requirement, since the process of Planning for the future requires a good Next State predictor. This by itself points out a weakness of the “perception as a window into reality” model, since that doesn’t involve any internal generation (and without generation we can’t solve any System 2 problem that involves prediction).
What does this have to do LLMs, since we have been talking about Next State prediction for all of this section? The Next State can be an image or it can be a piece of text, and as we learnt the two are equivalent. Hence the important question is whether an LLMs are able to develop an accurate model of the world based on their text only training dataset (assuming the dataset has been filtered so that it only has true propositions in the Wittgensteinian sense), which allow them to make good predictions. This is a hotly debated topic in the AI community today, with proponents on both sides. In my opinion LLMs indeed have this ability, with the caveats about the training data set and the ability to do continuous improvement as humans do. Several researchers have shown that LLMs develop internal models of the world in simpler environments such as board games, and there is some evidence that this continues to hold for general purpose LLMs trained on language data. Researchers have developed robots controlled by LLMs, that have the ability to plan out a sequence of Actions in the real world, before they attempt to carry them out.
What Would Kant Think of LLMs?
So we finally come to topic that was advertised in the title of this essay: What would Kant think of LLMs? I think Kant would be very pleased with LLMs, since they provide a further validation of his fundamental idea that the brain is essentially a reality generating machine (with the help of new data coming in from the Noumenon and some a priori concepts that we are born with) which is able to generate the rich picture of the world from the chaotic and sparse data that is coming in through our senses. Do LLMs also have this ability? We will examine this question next.
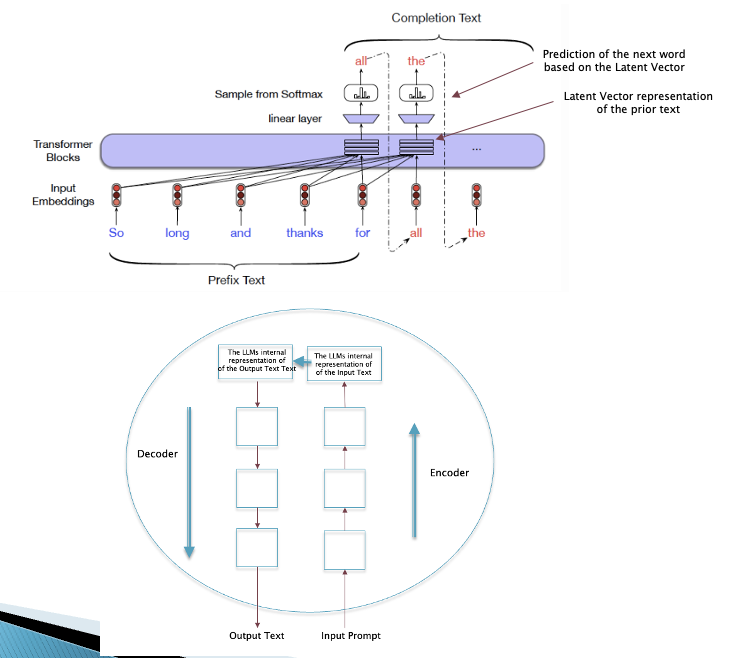
Figure 19
The top part of Fig. 19 shows the process of text generation using the LLM called Transformer. The input prompt into the model is shown on bottom left while the generated text is shown in the upper right. The input text is converted into a Latent Vector representation which is then used by the generation process, and this happens in a recursive manner on a word-by-word basis. This process can be further abstracted as shown in the figure in the bottom part of Fig. 19, and this has a direct correspondence to the operation of brain in Anil Seth’s (Kantian) model as shown in Fig. 5: The input prompt can be considered to be analogous to the sensory signals coming in from the noumenon. This information is mapped by the LLM into the language Latent Vector Space by the Encoder part of the LLM. The Decoder part of the LLM then takes the information in the Latent Vector and converts into another piece of text. In some sense the LLM is taking a piece of information that is incomplete or lacking detail, and then proceeds to supply the missing parts as part of the generated text. The same process happens for of images as shown next.
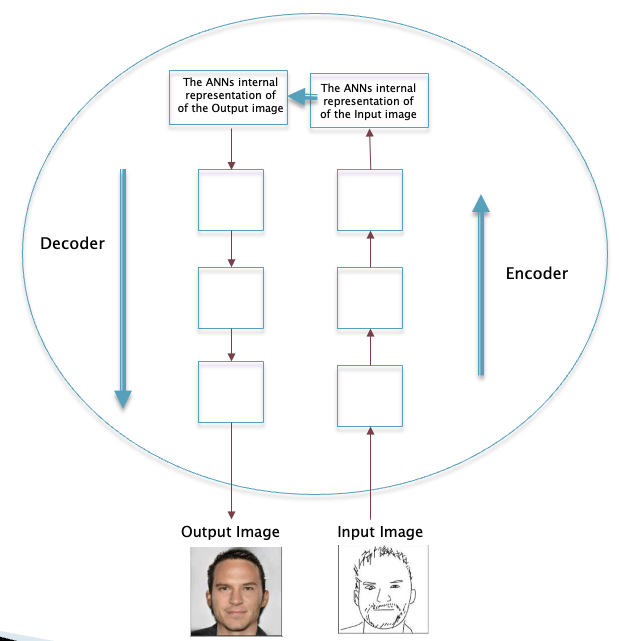
Figure 20
The process of image generation by an ANN is shown in Fig. 20. It takes in information that is rough or incomplete, such as a sketch of a human head, encodes it into a Latent Vector, and then maps it to another Latent Vector that represents a completed image with all the details, which is then decoded. Hence both language and image generation can be considered to be examples of filling in the rest of the pattern starting from rough or incomplete data. This is exactly the mechanism that Kant proposed for perception, with the incomplete information now coming in from the noumenon, which is then converted into the multi-colored high definition image of the world that we see in front of us.
As I pointed out earlier, the big difference between current ANNs and the brain is that ANNs are trained on a one-time basis and then put to work making predictions, while the brain undergoes continuous training. At the present time it is not practical to continuously re-train (or fine tune) ANNs, since they are housed in an expensive datacenters and serve a large number of users. Hence we cannot modify the ANN parameters based on any one users input prompts. In order to make the ANN more brain-like, we will have to personalize them to individual users, so that ANNs can be continuously fine tuned based on the prompts that the user is feeding into it. The recently announced ANN on the Apple iPhone is a step in that direction, though the local ANNs are currently much smaller and less powerful than the best server based models out there.
How about other aspects of Kant’s system that are also reflected in ANNs?
-
The Concept of Time: Kant said that time is an a priori concept that we are born with. Do LLMs develop the concept of time as a result of their architecture or training? I think that LLMs are able to develop this concept and part of the reason of this is ties to the architecture of Transformers. If you look at the top part of Fig. 19, it shows a sequence of text being fed into a Transformer. The Transformer architecture consists of a series of columns whose number is equal to the size of the word sequence being fed into it plus the size of the word sequence that it is generating. Each of these columns is a repetition of the same architecture which consists of a series of Self-Attention and Dense modules (which are also repeated in the vertical dimension). I think the concept of time arises as a combination of the fact that data is fed into the Transformer in a sequential fashion combined with the fact that it processes this data using a structure that sequentially repeats. In actuality the Transformer design has an additional mechanism on top of the base model which modifies the input vectors in an unique way as a function of their position in the sequence. This improves the performance of the system, but even without it the Transformer is able to work.
-
The Concept of Space: Space is another a priori concept that we are born with in Kant’s model and there are several aspects to our perception of space, such as: We are able to organize the mass of photons arriving at our retina into an orderly world with localized objects. Each of these objects is such that if it were to move from one location to another, or where to rotate around or placed in a different lighting, we would still recognize it is the same object. Can ANNs do this? It so happens that even the first generation of ANNs, called Multi-Layer-Perceptrons or MLPs, were capable of organizing the pixel data in their inputs into higher level representations for the various objects in their input. As a result when the networks were run on the reverse direction, so that now they were acting as image generators, then a rough approximation to the objects was regurgitated back. Convolutional Neural Networks or CNNs which came later, where much better at image processing, and they were able to do the same. Also the concept that an object does not change if it moves around the image is baked into the architecture of CNNs. However rotational invariance is not, as a result CNNs and other types of ANNs require a much larger number of training data before they form a good model for an object. Our brain is much more efficient at the task and is able to do the same based on just a few examples.
The concept of space and time are probably sufficient to enable ANNs to be able to perform tasks that are useful to us. But what about other aspects of our consciousness, such the perception of emotions, hunger, thirst, anger, joy etc.? These are more closely related to the aspect of consciousness, and clearly ANNs are not capable of any of these. Anil Seth in his book remarks that there is a difference between being intelligent and being conscious, and one can one of these properties and not the other. Full consciousness is tied to living beings, with its main objective to take all steps necessary to keep us alive. Clearly we don’t want ANNs to have this property for obvious reasons, and even if we did, we currently have no idea how to go about doing this. Hence humanity can make wonderful use of ANNs that are intelligent and make our lives better, without making them fully conscious.
In the meantime is there a chance that ANN systems can become consciousness as we make them bigger and bigger, as an emergent property? I think this is quite unlikely, and to understand why we need to go back to the ideas of Husserl, who told us that a model can never capture all aspects of reality. Our brain is in direct contact with the sensory information coming in from the noumenon, to which our models don’t have access. Moreover it is not clear that our perception of the brain captures all aspects of the organ, since it exists in the noumenon. Lastly the ANN models of the brain are nowhere as complex as the real thing, and we won’t be closing the gap anytime soon.