Artificial Neural Networks and the Scientific Method
Figure 1
Something wonderful happened to the human race in the 1600s. After being essentially flat for almost 2000 years (since the peak of the Roman Empire), the economic rate of growth suddenly took off in an exponential fashion, leading to the current world that we live in. The question is: What Happened? A leading candidate for the answer is, the Scientific Revolution. But science has been practiced since the time of the Greeks. What was so different about the way science was done post 1600 compared to the past?

Figure 2
This question was posed by Michael Strevens in his book “The Knowledge Machine”. In this post I will begin with a summary of his findings, and then try to connect this with the rise of Artificial Neural Networks or ANNs. After a long period of gestation, ANNs have suddenly started making progress in leaps and bounds and a big open question is whether they represent a fundamentally different way of doing science. And if so, what will it lead to? Is this a new exponential boost to our civilization?
Noah Smith discusses this question in this blog post, in which he referred to the Scientific Revolution as the Second Magic, and to Artificial Intelligence (AI) as the Third Magic (with Writing being the First Magic). In his opinion AI is a fundamentally new way of doing science compared to the original Scientific Revolution. I will critique this hypothesis, and propose that indeed there is a difference in the way is AI is done and what came before it, but at the root it is a continuation of the original Scientific Revolution, but using a vastly superior new tool.
Why Did Science Take Off After Newton?
So, what happened in the 1600s? The answer in one word is: Newton. Before Newton, scientists (or Natural Philosophers as they were then called), tried to find explanations for natural phenomena, but these explanations involved factors such as theological, aesthetic or philosophical considerations. According to Strevens, post Newton all these extraneous factors were thrown out, and the only thing that mattered was the agreement between predictions from the theory and empirical measurements. This new way of doing Science was actually proposed by Sir Francis Bacon in the early 1600s but was first rigorously put into practice by Newton.
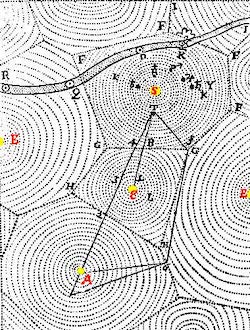
Figure 3: The Universe according to Descartes
As an example of a theory from before Newton, consider Rene Descartes theory of planetary motion. Aristotle back in the 3rd century B.C. tried to explain all motion, as an innate desire for objects to seek out their natural state, so in a sense he was ascribing a biological function to in-animate objects. Descartes, who lived just before Newton, started from the principle that nothing moves unless it is pushed, which is quite reasonable, and concluded that empty space between the planets is not really empty but is filled with particles that are pushing the planets along. Note that both these theories were based on philosophical beliefs of their originators and were scientific dead-ends, since they could not be used to make reliable predictions.
When Newton proposed in his Principia Mathematica that the planets move because of the force of Gravity that varied as the inverse square of distance, he was aided by several advances in the Astronomy that had taken place in the preceding century. Tycho Brahe had made very precise measurements of the motion of planets, which was quite a feat since he did it in the pre-telescope era. These measurements where then used by Johannes Kepler to propose his Three Laws of Planetary Motion, which were concise mathematical relations governing various aspects of planetary motion such as the shape of its orbit and the relationship between its distance from the Sun and its period of revolution. Newton realized that the Inverse Square Law can be derived using Keplers’s Laws, and also provided an explanation for all motion, not just in the heavens but also here on Earth. But there was one problem with this theory: The newly postulated force of Gravity seemed to be propagating through empty space from the Sun to the planets, which seemed to be hard to believe since, unlike Descartes’s theory, there was no agent that was pushing the planets along through direct contact. Newton dismissed this criticism, and his response, that is recorded in the second edition of the Principia from 1713 was, I do not feign hypothesis.
Newton was using the newly proposed Baconian Principle which stated that the only true test of a Scientific Theory is that its predictions should agree with experiment, and other considerations don’t matter. He clearly did not have an explanation for Gravity propagating through empty space, but he was saying that this did not matter since the theory had a such broad and powerful predictive power. Furthermore, he couched his theory in a few mathematical equations from which very precise predictions could be obtained. As pointed out by Strevens, this was the critical link that led to the Scientific Age. Henceforth, all Scientific Theories had to follow the template laid down in the Principia, even those from non-mathematical sciences such as Biology or Chemistry: The proof of whether a theory being proposed is correct is entirely based on its agreement with experiments and nothing else.
This was a highly irrational idea to grasp for people living in that age, who favored theological or common sense explanations for natural phenomena. A very important aspect of this way of doing science was that the scientist’s explanations for how he arrived at his theory did not matter. It could very well be that one could arrive at the right theory by using the wrong reasoning for it, as long there was experimental agreement, all was forgiven. Examples of this abounded in the centuries after Newton, for example Maxwell used Faraday’s ideas of elastic lines of force in a space filled with a substance called ether to arrive his theory of Electro-Magnetism. Later Einstein showed that neither assumption was necessary for the theory to hold.
A very good example of a more modern theory that sounds completely irrational, but nevertheless has excellent agreement with experiments, is Quantum Mechanics. Even 100 years after the theory was first proposed, scientists still don’t understand how light could both be a particle as well as a wave depending on the experiment being performed. Not only that, but the particle-wave duality extents to pieces of matter such as the elementary particles that make up the atom! There is no human-comprehensible physical picture that explains this phenomenon just as 400 years ago there was no good explanation for Newton’s idea of Gravity propagating through empty space. But the equations of Quantum Mechanics are the most precise descriptions that we have of the reality that we live in, even though we don’t understand why they work.
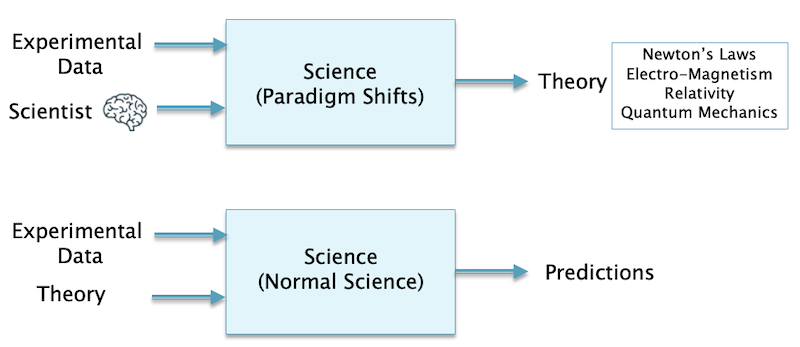
Figure 4
A summary of how the Scientific Method works for the case of the Physical Sciences is shown in the Figure 4, and it happens in two steps. As pointed out by Thomas Kuhn in The Structure of Scientific Revolutions, Science progresses when a new theory is proposed, examples of which are listed on the right hand side. This happens in the first step and requires a creative leap which Kuhn referred to as Paradigm Shift. Once a new theory becomes accepted then the second step kicks in, and the majority of Scientists carry out what he called Normal Science, which is defined as the process of working out the consequences of the theory for various problems. Paradigm shifts happen rarely, and are caused by the existing theory not being being able to make good predictions for some particular experiments. The base equations for the theory cannot be derived in the mathematical sense. In the Baconian spirit they are used since they make good predictions in the process of doing Normal Science.
A new Scientific Theory is usually proposed at a time crisis when the old theory starts to develop significant gaps with experiments. At these times scientists usually come up with more than one proposal to resolve the problems, and there follows a period of uncertainty. The process by which one of these theories wins out and becomes the established orthodoxy is called Baconian Convergence. As prescribed by Francis Bacon, the alternative theories battle it out with the only criteria of success being agreement with experiments, until one of them wins out. The current crisis in Physics with multiple competing theories for Quantum Gravity falls in this class.
The success of Physics in explaining natural phenomena post Newton has had an un-intended consequence. Since all Physical theories can be codified in a few ‘simple’ equations that can be used to explain a huge number of natural phenomena, we expect this to hold in other areas of knowledge as well. Hence scientists of the more theoretical bent are always searching for some simple underlying principle that can be used to explain complex phenomena. But this program has run into problems in recent decades, where there doesn’t seem to be simple theories in fields, other than Physics, that can explain a wide range of phenomena. Hence it could be that Physics is more of an exception than the rule in being able to capture the regularities in Nature with simple all encompassing theories that can be specified using just a few equations.
Are Artificial Neural Networks Science?
I am going to argue that the functioning of ANNs hew pretty closely to the original Baconian definition of what constitutes Science, but with an important exception: The equations in ANNs are no longer simple and elegant equations that we see in Physics, but are highly complex with hundreds of millions of parameters. But just as in Baconian Science, an ANN model lives or dies by how well its results agree with ‘experiment’.
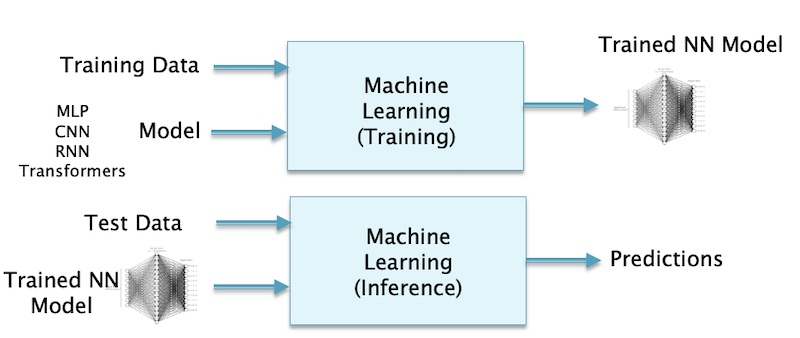
Figure 5
In analogy to the outline of the Scientific Method for Physics in the Figure 4, I have tried to sketch out the way the field of ANN operates in the Figure 5. Just as for the case of the classical Scientific Method, it progresses in two steps.
- In the first step an ANN model is chosen and then trained using a portion of the data that we are trying to model. Coming up with the structure of the model itself requires a creative leap, and these models have become more sophisticated over time. Some examples of models are MLPs (Multi-Layer Perceptrons), CNNs (Convolutional Neural Networks), RNNs (Recurrent Neural Networks) and Transformers. The chosen model is trained in step 1 using the training data, which is the process of estimating the parameters of the model. The algorithm that is used for this purpose is called Backprop and it is based on the Chain Rule of Differential Calculus.
- In the second step the trained ANN is used to make predictions on data that is separate (but similar to) to the training data using in Step 1. The trained model is judged to be good if its predictions turn out to be accurate. These predictions are statistical in nature, so the model provides probabilities of various outcomes, from which the final prediction is chosen.
A comparison of Figure 4 with Figure 5 shows that they are very similar. Both Physics Theories as well as ANN models are trying to capture regularities, whether in Nature, or in human generated systems such as language and images (for ANNs). In the case of Physics these regularities are summarized in the form of a few mathematical equations, while in the case of ANNs the regularities are captured in the interconnection topology of the ANN and in the strength of connections between its nodes. However in contrast to the Scientific Theory, the ANN model cannot be neatly summarized in a few basic equations, indeed the equations describing the complete ANN are too complex to even explicitly write down. Another difference is that a Scientific Theory only has a few parameters, the number of parameters needed to describe all of Physics is less than 50. An ANN on the other hand can have hundreds of billions of parameters. Indeed the whole point of training an ANN is to estimate these parameters.
In spite of these differences, they are both mathematical systems, and both prescribe to the same Baconian directive i.e., they are only as good as the predictions they make and will be discarded otherwise. The multiplicity of ANN models also shows that just like Scientific Theories, these models are also subject to the process of Baconian Convergence. For example Natural Language can be modeled using any of the ANN models listed in Figure 5, but the models have gotten better as we progressed from MLPs to RNNs to Transformers (Baconian Convergence was also seen in the process by which ANNs out competed other models of Artificial Intelligence such as Logic Programming and SVMs). ANN models have not been subject to Kuhnian Paradigm Shifts so far, but probably will be if they are to get to Human Level intelligence in the future.
A rap against ANN models is that they are Black Boxes, i.e., we don’t have any information about how they work or arrive at their predictions. But this state of affairs is not that different from models in Physics, since the base equations for those models were conjured ‘out of thin air’ by scientists such as Newton, Maxwell or Schrodinger. I would argue that the main difference between Physics models and ANNs, is that the former are much simpler since they can be written down in a few equations with only a handful of parameters while the latter is embodied in an ANN. However, in both cases we have a limited to no understanding of why the models work.
So perhaps the simplicity of Physics models reflects some deep structure found in Nature and is more of an exception to the rule. Human generated systems such as language or images, that are modeled using ANNs, also have a structure, but it cannot be reduced to a few elegant equations. However, in the last 20-25 years we have discovered that the regularity in these structures can still be captured using ANNs. This could be due to the fact that the human brain is a Neural Network as well, which has some similarities to ANNs. This imposes the constraint that a language or image is comprehensible to humans only if it can be understood and processed using a Neural Network of some sort.
The question of why the equations of Physics are simple was addressed by Daniel Roberts in his paper Why is AI hard and Physics simple? His conclusion was that the equations of Physics get considerably simplified due to two reasons: (1) Physical theories obey Spatial Locality, i.e., particles in the natural world only interact with other particles that are in their immediate vicinity, which limits the number of possible interactions each one of them can have, and (2) Physical theories are also translationally invariant, i.e., they work exactly the same whether you are on Earth or on Mars.
Is it Possible to Model Physical Laws Using ANNs?
If you see some regularity in nature, then in the usual way of doing Physics, you can try to derive the equations that explain your observations using one of the established theories. However, is it possible to arrive at these equations by using ANNs instead? This would entail feeding the experimental data into an appropriate ANN model that would then spit out the equations. If such a model were available to Kepler for example, he would have fed it Tycho Brahe’s observations and the model would give out his laws of planetary motion. This program of converting observations to physical laws has actually been implemented by Cranmer et.al. They used a type of ANN called Graph Neural Network to capture the inductive biases in the problem, followed by symbolic regression to fit the resulting model into an algebraic equation.
If you are curious about the converse question, i.e., can Physical Laws be used to Model ANNs? This was tackled by Roberts, Haida and Hanin in their book The Principles of Deep Learning Theory, in which they showed that simpler ANNs can be modeled using methods from Statistical Physics and the Renormalization Group Theory (the latter is one of the cornerstones of Modern Physics).
Conclusion
ANNs fit within the Baconian framework of doing Science but come with a fundamental new property: They do away with the idea of using mathematical equations to describe a theory, instead they capture complex patterns and regularities in their topological structure and in the strength of connections between their nodes. This is a new way of doing Science and opens up the Scientific Method to solving problems that could not be handled before. We are in the early stages of this revolution which may be as consequential to Humanity as the original Scientific Revolution.