Zeno’s Paradox of the Arrow

Introduction

Zeno of Elea was an ancient Greek philosopher who lived around 500 BC. He was a disciple of the philosopher Parmenides, who believed that all of reality consisted of an un-differentiated, unchanging motionless whole, which did not consist of any parts. Hence aspects such as motion, change and plurality were illusions according to him. In support of this point of view, Zeno came up with several paradoxes, which have continued to puzzle philosophers and scientists, even to the present day.

Fundamentally, these paradoxes drill through to the very base of aspects of reality such as the nature of time, space and motion, as well as the nature of infinity, so that their resolution requires a deep understanding of mathematics as well as physics. The level of understanding needed to resolve them didn’t begin to develop until the 17th century, with the development of infinitesimal calculus as well the revolution in physics that was bought about by Newton and his contemporaries. However a more complete resolution had to await the 19th century, in which mathematicians such as Cauchy, Weierstrass, Dedekind and Cantor laid the subject of calculus and the nature of infinity on a firmer mathematical footing. This state of affairs was shaken in the 20th century with the discovery of Quantum Mechanics, which upended our understanding of how microscopic particles behave which led to a re-evaluation of the paradoxes in the light of the Uncertainty Principle and the fact that matter seems to have both wave and particle properties.

Zeno showed that a phenomenon as common as motion, which most of us don’t think twice about as we go about our lives, is in actuality a deeply mysterious thing. Two thousand five hundred later, we still haven’t completely plumbed the depths of understanding of what time, space and motion really are. In this essay we will focus on one of Zeno’s paradoxes, called the Paradox of the Arrow, and we will trace how our understanding of this paradox has changed since the time of Zeno, and continues to evolve even today.

Zeno’s Paradox of the Arrow

Consider an arrow that is in flight from point A to point B in space, and assume that its tip passes through point C on the way. Also assume that it passes through these points at time $t_A, t_B$ and $t_C$ respectively. We will assume that all time instants and points in space are atomic in nature, so that they cannot be sub-divided into smaller parts. The question that Zeno asked is the following: Can we tell if the arrow is in motion at any one of these time instants between $t_A$ and $t_B$? Let’s assume that the arrow occupies a set of points in space at time $t_C$ which correspond to the shape of the arrow. In order to be in motion at that instant, the arrow will have to occupy space that exceeds the size of the arrow. But this leads to the conclusion that arrow will be in two different places at the same instant of time, which is an absurdity. From this Zeno concluded that at any atomic instant of time, the arrow is actually at rest, i.e., not moving. So if we now look at the all instants of time that lie in the interval $[t_A, t_B]$, then at any one of those instants the arrow is at rest. Then the question arises, how does the arrow get from point A to point B? This is a paradox since in reality we do see that the arrow is moving.

Fundamental to the statement of the paradox is the notion of atomic instances of time. Aristotle was one of the first philosophers who tried to resolve the paradox, and he did so by questioning whether these instances do in fact exist. He suggested that time is instead made up of continuous intervals of finite duration, and during these intervals the arrow is indeed allowed to travel through space. This was not a wholly satisfactory resolution, since mathematically speaking, one can easily define an instant of time, it is just a number, but what is an interval? If it is in turn made of atomic instants, then it should be further dividable. Morever if an interval is be made up of an infinity of these atomic time instances each of duration zero, then again, how can a finite duration arise from an infinity of these time instances? One can see that the paradox of the arrow is really a question about the deep nature of time and space, and also the nature of infinity, questions that were not resolved until the 19th century. It is said that the Ancient Greeks where so disturbed by these paradoxes that they completely avoided the mention of infinity in their development of mathematics and science, most of which happened after the time of Zeno. This prevented them developing infinitesimal calculus, even though they had all fundamental concepts needed to do so.

The arrow paradox raises several questions, that are all related to each other:

If we confine ourselves to the mathematical world, we can clearly go about subdividing an interval into smaller and smaller parts, and continue to do this indefinitely. But is this is something that can be done in the real world, either to space or to time? So the pradox also raised questions about the true nature of reality its relation to mathematics. These questions stumped philosophers, until the first glimmerings appeared with the Scientific Revolution in the 17th century.

How Can an Object be in Motion?

The paradox of the arrow asks the question: How the arrow can be in motion if it is motionless at any one time instant? The discovery of infintesimal calculus gave scientists a tool that they could use to probe into this problem. The attack on the problem happened in two phases: Phase 1 was in the 17th century when calculus was discovered by Newton and Leibniz and Newton then applied it in coming up with his Three Laws of Motion. However as we show below, their solution to the problem was not entirely satisfactory, and a fuller resolution had to wait for Phase 2 which happened in the 19th century, when subject of calculus was put on firmer theoretical foundations.

Galileo, Newton and others introduced the concept of the average velocity of an object, which was defined as follows:

\[v_{avg} = {\delta x\over{\delta t}}\]

where $\delta x$ is the distance covered by an object over a time duration $\delta t$. If this calculation is carried out for time intervals that infintesimally small, then $v_{avg}$ becomes the instantaneous velocity $v(t)$ at some time instant t. Hence $v(t) = {\delta x\over{\delta t}}$ for the case when $\delta t = 0$. They introduced the important idea that the velocity of an object can be can be well defined even for atomic instants of time. Thus when the arrow travels between points A and B, then at every time instant between $t_A$ and $t_B$, it has a well defined velocity, even though at any particular time instant it is seen to be completely stationary. Hence according to Newton, Zeno was right that arrow is stationary at any one instant of time, however it does not follow from this that it has zero velocity, since velocity can be defined even for individual instants of time.

This use of differential calculus in physics worked well in practice, it enabled scientists to compute velocities and higher order quantities such as acceleration. However it side stepped the problem that Zeno had raised, of whether time progresses in instants or in intervals. Also Newton had a simple solution to the problem of where the arrow was located in between two time instants which was his First Law of Motion: In the absence of a force, the arrow will keep moving at a fixed velocity, so that at time instant t, it is located at $x(t) = vt$ units from the starting point. Even in the presence of a force, such as gravity, Newton and Galileo came up with the formula

\[x(t) = {1\over 2} gt^2\]

for the location of the arrow. These formulae enable us to compute the location of the arrow at arbitrary instants of time.

Newton and Leibniz’s definition of the derivative involves very small, but finite, time intervals, which are set to zero in order to get the final answer. However this leads to the mathematical problem of dividing by zero. Indeed in part of the calculation $\delta t$ is treated like a very small but finite quantity, while in other parts of the calculation its value is to set to zero. For example consider the case when motion is defined by the equation $x(t) = t^2$, as a function of time. Then

\[\delta x = x(t+\delta t) - x(t) = (t+\delta t)^2 - t^2 = 2t.\delta t + {\delta t}^2\]

so that

\[v_{avg} = {\delta x\over{\delta t}} = {2t.\delta t + {\delta t}^2\over\delta t}\]

If we treat $\delta t$ as a finite quantity such that $\delta t > 0$, then we can divide the numerator and denominator by this quantity to get

\[v_{avg} = {2t + \delta t}\]

Newton and Leibniz’s methodology called for setting $\delta t = 0$, to get the final answer

\[v(t) = 2t\]

Notice how $\delta t$ was simultaneously treated as a quantity that is non-zero in the first step (in order to avoid dividing by zero), AND it was set equal to zero in the second step. Hence Newton and Leibniz side-stepped the important question that Zeno had posed about the nature of time, by treating it as both continuous and discrete during the course of their calculation. If they had shown this calculation to Zeno, I am sure he would have dismissed this as the wrong resolution to his paradox for this reason.

Newton or Leibniz didn’t have a solution to the problem of obtaining a more rigorous definition of the derivative, and the first steps in this direction had to wait for the French mathematician Augustin-Louis Cauchy in the 1820s, when he introduced the concepts of limits and convergence of a series into calculus. Later, in the 1860s The German mathematician Karl Weierstrass fully developed these ideas and gave the definition of the derivative which is still in use today. According to Weierstrass the velocity $v(t_1)$ at time instant $t_1$ is given by

\[v(t_1) = \lim_{t_2\rightarrow t_1}{ x(t_2) - x(t_1)\over{t_2 - t_1} }\]

The $\lim$ or limit operation is defined as follows: For every $\epsilon >0$, there exists a $\delta >0$, such that if $\vert t_2 - t_1\vert < \delta$, then $\vert x(t_2) - x(t_1)\vert < \epsilon$ (where $\vert t\vert$ is defined as the absolute value of $t$). When put in words, this definition is saying that we can make $x(t_2)$ as close as we want to the initial point $x(t_1)$, by choosing the instant $t_2$ to be sufficiently close to $t_1$. In other words, if we want the distance between $x(t_2)$ and $x(t_1)$ to be less than a tiny amount, say 0.0000000001, we can always find a $t_2$, a tiny distance away from $t_1$, that makes this possible.

Hence the velocity $v(t_1)$ at time $t_1$ is defined as the limit to the sequence of average velocities ${x(t_2) - x(t_1)\over{t_2 - t_1}}$, as the time instants $t_2$ gets closer and closer to $t_1$. Note that $t_2$ can approach $t_1$ from either the left or the right, and the derivative is well defined only for the case when the resulting two limits are equal. In this definition of the velocity we are no longer dividing by zero, and instead define the derivative as the limit of a convergent sequence, and this limit always exists if the function $x(t)$ is continuous at point $t$ (i.e., there are no jumps in the function at time $t$).

Note that this definition does not involve the concept of intervals or infinitesimals of either time or space, everything is in term of individual instants of time and points in space. It assumes that the next point $t_2$ can be made as close as we wish to $t_1$, without ever actually ‘touching’ it. This points to another important concept that was introduced into mathematics at this time, which is that of the continuum. An interval of time (or space) forms continuum, if between any two points, one can always find an infinity of points, no matter how small the interval between them.

Once the idea of differentiation was put on a firm theoretical basis, Zeno’s paradox of the arrow had the following resolution: Zeno was right in stating that arrow was stationary at any one time instant, however he was wrong in concluding from this that the arrow does not move at al. In fact the arrow possesses a finite velocity, which can also be defined at atomic instants of time by using the concept of the derivative of a function. However, to make the distinction between being at rest and movement requires that we examine the arrow not at a single point in time, but at least for two points. Hence within this framework motion is the process of occupying different points in space at different points in time. Notice that this definition introduces a new player, which is that of an observer who actually registers the movement. Hence motion is not an intrinsic property of the arrow, but is relative to an observer. We will later see that Quantum Mechanics made this idea of an observer critical to understanding other properties of matter, not just motion.

This resolution to the paradox does the job mathematically speaking, but does it agree with our intuitive sense of movement? Math is telling us that movement consists of being at a successive set of points in space at successive times, but what is happening in-between those points, is this were the movement is actually happening? We can try to pin down the arrow’s trajectory by looking at intermediate instants of time, for example if $t_C = {t_A + t_B\over 2}$, then the arrow will be at the point $x(t_C)$ at $t=t_C$. But this not enough to pin down the motion, since we still don’t know how the arrow got from $x(t_A)$ to $x(t_C)$. We can continue this procedure of halving the time intervals ad infinitum, but however many times we do it, it is still impossible to pin down the instant at which the arrow is actually moving, since there is always a gap between successive points!

This description of the arrows flight implicitly assumes that both space and time are made up of discrete points, so that the arrow is moving from one discrete point to another as time progresses. This is clearly not a satisfactory picture, since given the starting point $x(t_A)$, clearly there is no ‘next’ point that the arrow can go to, since if there was any such point, one can always find another point that is closer to the starting point by using the halving procedure. This means that trying to understand the movement of the arrow, as something that is moving from point to point in space, does not make sense. The arrow is in fact moving over the continuum of points, which is why it is impossible to find out the point where it will be at the very next instant, since the next instant does not exist in a continuum.

We can make the successive points as close together as we like, since space and time are both continuums. It turns out, that this is as close as we can get to picturing movement. Note that movement is actually happening over a continuum but our brains have a great deal of difficulty picturing this. We are more comfortable with points in space, and starting from a point we look for the next point in space that the arrow will occupy. However math is telling us that there is no next point! But this does not mean that movement cannot happen. The arrow does move, but its moving over a dense continuum of points which we can’t visualize very well. Not only we can’t visualize it, but when this idea was first introduced by Cauchy, Weierstrass et.al., even mathematicians had a poor understanding of what a continuum is.

Thus it can be said that Weierstrass banished the idea of a quantity that is infinitely small, i.e., the infinitesimal, from mathematics, but in order to do so he had to introduce the idea of the infinitely large, for this is what the continuum is with its infinity of points. The latter half of the nineteenth century was spent in trying to clarify the nature of the continuum, and names most closely associated with this are that of Richard Dedekind and George Cantor. This is covered in the next section.

Motion in the Continuum

The problem of the continuum can be connected to another one of Zeno’s paradoxes called the ‘Paradox of Plurality’, and it reads as follows: If the arrow moves from point A to point B, then how can we compute the distance over which it has travelled? Assuming that A coincides with the origin of the number line at 0, and the B is located 1 unit away, then clearly the arrow has travelled for 1 unit of distance. Now lets split up the segment [0,1] into two parts at the midpoint, so that the arrow travels from [0,0.5] and then from [0.5,1]. The total distance it travels is still 1, which we obtain by adding up the two segments. If we further divide up the two halves in two we get 4 segments. We can continue this splitting process in-definitely, until we get an infinite number of line segments between 0 and 1. Zeno then presented the following paradox: Assuming that the infinity of the resulting segments can be added together, does it still add up to one? If the length of the infinitesimal segments in the limit is zero, then the sum will also be zero. On the other hand if the infinitesimal segments have a non-zero length, then the resulting sum will be infinity. Since neither of these two options are equal to the actual length of the segment, so where is the error in the logic?

The fundamental problem here is that of defining the sum for the infinity of points that exist over the continuum [0,1]. Clearly the sum of the infinitesimal segments should add up to 1, but how can this happen if each of them has length zero? It turns out that trying to resolve this paradox is another very difficult problem having to do with the concept of infinity, and one that was not solved until the latter half of the 19th century and this was done by the German mathematicians Richard Dedekind and George Cantor. In order to solve the problem, they first had to figure out the nature of the numbers that existed in the continuum, and this was done by Dedekind. He gave a construction of numbers that are irrational (i.e., cannot be expressed as ratios of integers), and the union of all the rational and irrational numbers constitutes the continuum. Examples of irrational numbers include those that can be written as the root of rational numbers, such as numbers such as $\sqrt{2}$, and these are called Algebraic Irrationals. There is another set of irrationals that cannot be expressed in this way, and these are called Transcendentals, examples include the numbers $\pi$ and $e$. When expressed as a decimal, irrational numbers have a never ending series of non-repeating digits after the decimal point. Dedekind showed that once that irrationals are included on the number line, the line becomes dense, i.e., it is now a continuum, with no ‘holes’ in it. The resulting numbers are called Real Numbers.

The nature of infinity and that of the continuum was further clarified in a brilliant series of papers in the 1870s by George Cantor, specifically he was able to prove the following:

Cantor’s discoveries pointed to the fact that number of points in an interval is not a good indication of the length of the interval, since intervals of different sizes can have the same number of points (and whose cardinality is equal to c). If the number of points in an interval of the continuum cannot be used to characterize it, what is a good indicator of the length of an interval in space or the duration of time? This problem was solved a few decades later, around the turn of the 20th century, and the main contributors to it were the French mathematicians Emile Borel and Henri Lebesgue. They generalized the notion of the length of an interval, into a quantity that they called measure, so that their work is called Measure Theory. The measure of simple open segment $[a,b]$ is simply $a-b$, however they were able to extend this concept to more complex sets. In particular they showed that the measure of a de-numerably infinite collection of segments, is the sum of their individual measures, so that

\[m(\sum_{i=1}^{\aleph_0} X_i) = \sum_{i=1}^{\aleph_0} m(X_i)\]

Going back to the line segment [0,1], clearly $m[0,1] = 1$. What about the measure for the set of all the Rational Numbers in [0,1]? Since the measure of any individual number is zero, it follows that if $Q_i$ is the $i^{th}$ rational number in the interval [0,1], then

\[m(\sum_{i=1}^{\aleph_0} Q_i) = 0\]

Note that this summation is allowed since the set of Rational Numbers is denumerably infinite according to Cantor. From this it follows that

\[m([0,1]) - m(all\ rationals\ in\ [0,1]) = m(all\ irrationals\ in\ [0,1]) = 1\]

Hence the irrationals that are left over after all the rationals have been removed, have measure 1. This is an amazing result, since it is saying that the non-denumerable infinite sum of all the irrational number that exist over this interval has a finite measure, even though each number individually has measure zero. This result resolves Zeno’s Plurality Paradox, since the set of points that are removed from the line segment during the halving procedure is a subset of the set of rationals. Hence if the arrow were to traverse the segment [0,1] by taking an denumerable infinite number of tiny steps between neighboring rational numbers, it would still travel a total distance of 1 unit.

The development of Measure Theory further led to a rigorous definition of the integral by Lebesgue which is still in use today, the so called Lebesgue Integral. In order to see the connection between Measure Theory and the integration, note that the calculation that we just did can also be written as the integral

\[m(all\ irrationals\ in\ [0,1]) = \int_{0}^{1} v(t) dt = 1\]

where the function $v(t)$ is given by: v(t) = 0 if $t$ is a Rational Number, and 1 otherwise. Older definitions of the integral, such as the one given by Bernhard Riemann, were incapable of integrating these type of complex funcions.

In the last section we saw how the theory of differential calculus was put on a firm theoretical footing and this resolved Zeno’s Paradox of the Movement of the Arrow, while in this section we see how the theory of Integral Calculus reached its current rigorous development after resolving the related Paradox of Plurality. The resolution of these two paradoxes together led to our current understanding of the mathematics of the infinitely small, and the infinitely large.

I find it fascinating to think that a Greek Philosopher from 500 BC hit upon the fundamental issues that lie at the heart of calculus. The Greek mathematicians who came after him were sticklers to logical rigor, hence refused to develop calculus any further, without first resolving the paradoxes. Two thousand years later, Newton and Leibniz had no such qualms, and they went ahead and developed the basics of calculus without first figuring out what an infinitesimal was, and thus launched the Scientific Revolution.

Now that we have a mathematically rigorous definition of the continuum, does it make it easier to visualize motion over the continuum? Well no, since our brains are still wired to think of motion as a discrete set of positions at discrete points in time. But now, thanks to the efforts of the 19th century mathematicians, we can be sure that arrow is actually travelling over the continuum, even though we can’t actually observe it doing so (since there is always a gap between any two observations). But does it make sense to talk of motion of the arrow in these gaps at the instants that it is not being observed?

This raises the mystery of what exactly is the arrow doing in-between two such observations. If we go by Newton’s Laws of Motion, then the position (and velocity) of the object can be predicted once we know its initial position, velocity and the forces acting on it. In particular in the absence of any force, an object moving at a particular velocity will keep moving at the same velocity. This would allow us to predict its position, even though it is not being observed. Is this what happens in the real world? If we were to drill down to a very small object, and try to observe its motion over very small intervals of time, what do we see? If the arrow were replaced by a fundamental particle, say the electron, can we carry out an experiment using a very powerful microscope, in which we try to see how it behaves while its moving over the continuum? Such an experiment was indeed carried out about a hundred years ago, and the results only deepened the mystery. This topic is discussed in the next section.

Quantum Mechanics and the Paradox

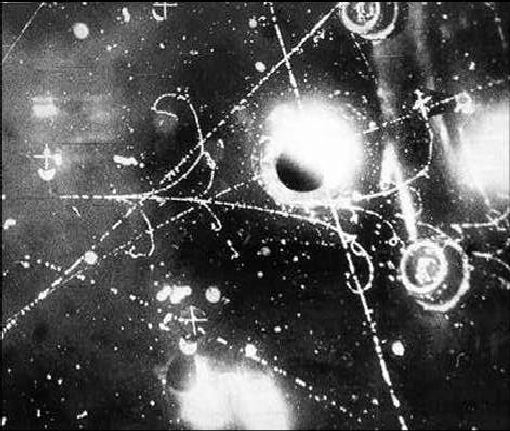
Figure 1

The photograph in Fig. 1 shows the path of several elementary particles as captured in a device called a Bubble Chamber. If we focus on the path of any one of these particles, we can see that it consists of a series of white dots. These are points at which the particle is interacting with the contents of the Bubble Chamber, and so these dots can be regarded as a series of observations that fix the position the particle at successive time instants. What is the particle doing at times that are in-between two of the white dots? If we go by Newton’s Laws of Motion, the particle will be located at a position whose value can be determined exactly since the particle’s velocity is also known. On the other hand, Quantum Mechanics has a very surprising answer to this question: We cannot have a precise determination of the particle’s position while it is in the space in-between area two observed positions. The only way to do would be take another measurement in the gap interval, which would have resulted in another white dot along the particle’s trajectory in Fig. 1.

When an object traverses a certain distance, we are only observing it at discrete instants of time. This is not so obvious when looking at the movement of a macroscopic object like an arrow. Newtonian Mechanics helps us interpret hat happened at the instants in-between two observations. Given the mathematical picture of a dense interval of points on the continuum, we can predict the location of the arrow with any amount of precision, at any time instant (even though the arrow was not being observed at that instant).

This raises the question: Does the particle move along a dense continuum of points when it is in the gap between two observations, as 19th century mathematics would have us believe? Quantum Mechanics tells us that the answer to this question is No!. The particle does not exist as a particle, or what we understand to be a particle, in-between two observations. In order to pinpoint its location at a certain time, we actually have to observe it that instant, and we can make successive observations intervals as small as we wish. But, there is always a gap between any two observations, since the observations are at most denumerably infinite, i.e., they can never be dense in the sense of the Real Number line. Hence the gap leads to an in-between segment of space, and the question arises: What is the particle doing while it is in these gaps? Quantum Mechanics tells us the following:

So the conclusion is: There is something that is moving in the continuum that forms the gap between observations (since Schrodinger’s equation is a differential equation from calculus, which pre-supposes the continuum), but it is not what we understand to be a particle. Hence the particle cannot be visualized while it is in-between two observations, it exists as a particle only at the most countably infinite number of points when it is being observed.

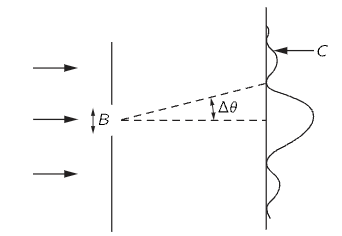
Figure 2

In order to get a better understanding of the situation, consider what happens when elementary particles such as electrons behave when passing through a screen with a single slit. When an electron passes through the slit, it’s position becomes known with an uncertainty that is equal to the width of the slit, so this is like making a rough measurement to determine the particle’s position. The electron then strikes a photographic plate placed after the screen, at which time its position once again becomes known. But what happens in-between the slit and the plate, where is the particle located at those times?

This is analogous to the question we asked about the arrow’s behavior between two successive measurements or the question about the location of the elementary particle between two successive white dots in Fig. 1. Quantum Mechanics tells us that in between two measurements, the particle essentially does not exist ‘in the form of what we normally think of as a particle’. Then what does it look like? The short answer to this question is: We don’t know. The particle definitely exists as a particle at the exact time that the measurements are made, that much we know for sure since we can observe it at those instants.

The only way to talk about the particle in between two successive measurements is by using the equations of Quantum Mechanics and Quantum Field Theory, and here is what the math is telling us: All of space is permeated by a ‘particle field’, which you can think of as similar to the electromagnetic field but for matter. This matter field contains energy, and this energy is not diffused throughout space, but is concentrated in energy quanta. These quanta of energy is what we observe as particles. Electrons are the energy quanta for the electron field, just as photons are the energy quanta for the electromagnetic field.

It is possible to extract information about the location and momentum of these energy quanta, but not both at the same time. If the uncertainty in its location is $\Delta x$ and the uncertainty in its position is given by $\Delta p$, then these two are connected by the following equation, first derived by Werner Heisenberg

\[\Delta x \Delta p \ge {h\over 2\pi}\]

where $h$ is Planck’s constant. Hence if a particle’s position is completely known, then we can have absolutely no information about its momentum and conversely if its momentum is known exactly, then it can be located anywhere in space.

Going back to the single slit experiment in Fig. 2, when the particle approaches the slit, it has a momentum in the horizontal direction but not in the vertical direction. However by going through the slit it acquires a momentum in the vertical direction as we see next. When the particle goes through the slit, the uncertainty in its vertical location is $\Delta y = \pm B$ where $B$ is the width of the slit. Hence the Uncertainty Principle tells us that there is also an uncertainty in the component of its momentum in the vertical direction given by

\[\Delta p_y \ge {h\over 2{\pi B}}\]

This uncertanty in the y momentum causes the trajectory of the particle of spread out after the slit. However this still doesn’t explain the diffraction pattern that we observe on the photographic plate, if this were a classical particle there would be no null points in the pattern, It turns out that the null points are exactly what we would observe if this experiment where to be carried out with light waves (or any other kind of wave) instead of particles. Here is a short explanation for this (taken from Feynman, Volume 3): The vertical momentum $p_y$ has a spread equal to $p_0 \Delta\theta$, where $p_0$ is the horizontal momentum $\Delta\theta$ is the angle at which the first null occurs. How can we compute $\Delta\theta$? Assuming that we are talking about waves, the first null occurs at an angle at which waves from edge of the slit have to travel one wavelength farther than the waves from the other edge, from which it can be shown that $\Delta\theta = {\lambda\over B}$, where $\lambda$ is the wavelength (this formula arises from the Theory of Wave Diffraction, for example see Chapter 30 of Feynman, Vol 1). From this it follows that $\Delta p_y = {p_0\lambda\over B}$. Hence if we were to pin down the position of the particle more exactly by making the slit narrower, i.e., reducing B, then the diffraction pattern spreads out more, i.e., the $y$ component of the momentum becomes even larger. Also $\Delta p_y B = p_0\lambda = h$. The last equation follows from the De Broglie formula for matter waves. Hence we have recovered the Uncertainty Principle since B is the uncertanty in the vertical position.

This experiment shows that in-between the two measurements, the particle no longer exists ‘as a particle’, it has acquired wave like properties! How can this be so? We don’t know. All that we can say is that the mathematical equations that this mysterious entity obeys, is similar to that of a wave propagating through space.

Going back to Zeno’s paradox, Quantum Mechanics tells us that a particle exists as what we understand to be a particle, only at the times at which it is being observed. Nobody has seen what a particle looks like while it is transitioning between two observations, since as soon as we observe it, it becomes a particle! This goes back to the conundrum we had raised in previous sections about trying to visualize the actual motion of a particle, as opposed to just saying that it is at spot A at time $t_A$ and at spot B at time $t_B$. Quantum Mechanics is telling us that this is as close as we can get in describing motion, since the particle exists as a diffuse wave like entity in-between two observations.

Another way of describing this situation is as follows: A particle in itself does not possess properties such as location or velocity. These properties only come into existence when the particle is being observed, i.e., interacting with an observer. When the particle is not being observed, its properties are indeterminate. This raises questions whether these properties are in some sense the creation of the observer’s mind. This line of thought is further explored in the next section with regard to Immanuel Kant’s work.

In the original paradox, Zeno concluded that the particle is not moving at all at any instant of time. Calculus told us that the particles does move, but at any particular instant it is stationary and the only way to tell that it is moving is by observing it at two different instants. Quantum Mechanics also tells us the same thing, with the caveat that the particle assumes wave like properties in the gaps in-between observations.

Quantum Mechanics also tells us that the particle only changes state at the times when it is not being observed. This raises the following interesting question: If the particle is stationary at the instant of observation, what if we were to observe it with an extremely high frequency, almost like continuously observing it? Quantum Mechanics says that in this situation the particle won’t change state, for example if it were stationary, then it will continue to be stationary and motionless (since a state change is triggered by the act of non-observation). This is known as the Quantum Zeno Effect and has been observed experimentally (sometimes paraphrased as: A watched quantum kettle never boils!).

Philosophy and Zeno’s Paradox

Not only did the paradox play a very influential role in the development of calculus, as well as our ideas about the nature of infinity, it also had a big influence on modern philosophy. The great philosopher Immanuel Kant, who did most of his work in the late 1700s, spent time thinking deeply about Zeno’s paradox, and the conclusions that he drew from this investigation led to his ground breaking work Critique of Pure Reason.

Kant concluded that there is a difference between the world as it exists in reality, which he called the Noumenon, and the picture of the world that our mind presents to us, which he called the Phenomenon. Our brain is constantly getting bombarded with sensory data, and fortunately it has figured out a way in which the chaos can be organized, and this is by arranging events so that they are spread out in time, and exist in space. In his view space and time are not real things that exist in reality or the Noumenon, but are creations of our minds. Hence they are more like a frame of reference or a stage on which everything else happens. He also concluded that treating space and time as real things leads to Zeno’s paradoxes. For example Zeno’s Paradox of Plurality requires us to chop up a segment of space into infinitely small pieces. But the idea of sub-dividing an object infinitely many times is an idea from mathematics not from real life, since in practice something like that can never be carried out. But Zeno assumed that this could be done, thus leading to the paradox.

Kant was the first of the modern philosophers to raise doubts about the true nature of space and time. These ideas later had a big influence on the development of Quantum Mechanics. Kant served as a source of inspiration for Heisenberg, who it is said kept a copy of Kant with him at the time he was coming up with his ideas. Heisenberg in some sense extended Kant’s ideas further, by denying the real existence of even the material particles like the electron (in the form that we understand to be a particle). Thus the electron exists as a particle only at the time we are observing it, and at other times it exists as a diffuse wave like entity. So in some sense it can be said that the world exists and evolves in time in the Noumenon, to which we don’t have access. It becomes visible to us when we look at it, but only at the instant of the observation.

The Future of the Paradox

We can see that Zeno’s Paradox has inspired some of the deepest ideas that we have about the nature of space, time, motion and the concept of infinity. I find it amazing that the speculations of Ancient Philosopher who lived at the very dawn of civilization, have led to so much progress in human knowledge. To compete with this kind of immortality, can you think of a question or paradox that people will still be talking about 2500 years from now?

We still don’t know about the ultimate nature space. Does it exist as discrete atoms, like matter? If so, when a particle is moving in space, is it hopping from one atom of space to another? These are questions that Zeno thought about, and to which we still don’t have an answer. The equations of Quantum Mechanics and Quantum Field Theory are Partial Differential Equations, hence they assume that time and space can be modeled as a dense continuum of points. But perhaps these equations are approximations to more fundamental equations an even lower level of reality, that model time and space as discrete. There are proposals such the Theory of Quantum Loop Gravity that are headed in this direction.

We have replaced one paradox by another: How can an object be in motion and not in motion at the same time to, how can an object exhibit both particle and wave like properties?